Реферат: Математические методы планирования экспериментов
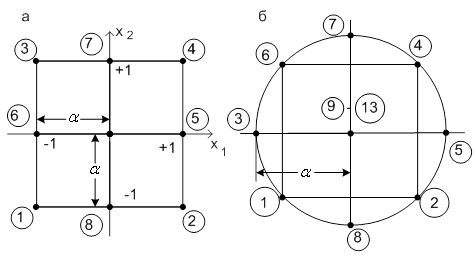
Рисунок
3 – Планы второго порядка при 
: а – ортогональный;
б – рототабельный
Таким образом, в общем случае ядро
композиционного плана составляет при 
ПФЭ 
, а при 
- дробную реплику от него. Если
линейное уравнение регрессии оказалось неадекватным, необходимо:
1) добавить (2 – k)
звездных точек, расположенных на координатных осях факторного пространства 
где 
- звездное
плечо, или расстояние до звездной точки;
2) провести 
опытов при значениях
факторов в центре плана.
При k факторах общее число опытов в матрице композиционного плана составит:
(8)
При этом величина звездного плеча 
и число опытов
в центре плана 
зависит от выбранного вида
композиционного плана.
Композиционный план для 
и 
представлен в
таблице 1.
Таблица 1 – Композиционный план второго порядка
| Номер опыта | Факторы | Результат | ||||||
|
|
|
|
|
|
|
|
||
|
Ядро плана |
1 2 3 4 5 |
+1 +1 +1 +1 +1 |
- 1 +1 - 1 +1
|
- 1 - 1 +1 +1 0 |
+1 - 1 - 1 +1 0 |
+1 +1 +1 +1
|
+1 +1 +1 +1 0 |
|
| Звездные точки |
6 7 8 |
+1 +1 +1 |
0 0 |
0
|
0 0 0 |
0 0 |
0
|
|
| Центр плана | 9 | +1 | 0 | 0 | 0 | 0 | 0 |
|
