 Дипломная работа: Разработка математической модели и ПО для задач составления расписания
Дипломная работа: Разработка математической модели и ПО для задач составления расписания
Эти идеи послужили основанием прямого алгоритма в целочисленном программировании:
Шаг 0. Начать со столбцовой таблицы, в которой ai0![]() 0 (i
0 (i![]() 1) и все элементы a0j, aij
и ai0 – целые.
1) и все элементы a0j, aij
и ai0 – целые.
Шаг 1. Проверить выполнение условий a0j![]() 0 (j
0 (j![]() 1); если они выполнены, то конец,
текущее базисное решение оптимально; если нет – перейти к шагу 2.
1); если они выполнены, то конец,
текущее базисное решение оптимально; если нет – перейти к шагу 2.
Шаг 2. Выбрать ведущий столбец s с a0s< 0. Выбрать строку v по правилу проверки отношения ai0/ais среди строк с ais> 0. Эта строка служит производящей для отсечения Гомори.
Шаг 3. Получить отсечение Гомори из производящей строки и
дописать ее внизу таблицы, т.е. добавить к ограничениям задачи уравнение (23),
где ![]() .
.
Шаг 4. Произвести преобразование таблицы, используя отсечение (23) как ведущую строку. Слабая переменная sk в (23) станет небазисной. Вернуться к шагу 1.
Доказательство конечности алгоритма см. [2], стр. 346-353.
Поскольку выбор производящей строки является задачей нетривиальной, по-видимому, должно существовать несколько строк, которые могут служить в качестве производящих. В предварительных рассуждениях в качестве производящей строки использовалась ведущая строка симплекс-метода. Эта строка всегда дает отсечение, которое является ведущей строкой с ведущим элементом, равным единице. По-видимому, в таблице существуют и другие строки, из которых могут быть получены отсечения с такими же свойствами. Допустим, что отсечение получается по формуле:
|
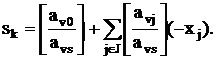
Строка v может стать производящей тогда и только тогда, когда
|
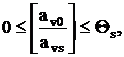
где ![]() определяется из условия
определяется из условия
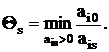
Определим множество V(s) как совокупность строк, удовлетворяющих условию (25).
Следующие два правила представляют собой примеры допустимых правил выбора производящей строки:
Правило 1.
1. Составить последовательный конечный список индексов строк таким образом, чтобы индекс каждой строки вошел в него по меньшей мере один раз. Перейти к 2.
2.
Если список пуст или не содержит
ни одного индекса из V(s), вернуться к 1.; в противном случае найти в списке первый индекс v![]() V(s). Выбрать строку v как
производящую. Вывести из списка индекс v и все предшествующие ему
индексы. Перейти к 3.
V(s). Выбрать строку v как
производящую. Вывести из списка индекс v и все предшествующие ему
индексы. Перейти к 3.
3.
Последовательно выбирать строку v, взятую в 2.,
как производящую, до тех пор, пока v![]() V(s). Как только v
V(s). Как только v![]() V(s), вернуться к 2.
V(s), вернуться к 2.
Правило 2.
1.
Пусть Vt(s) – множество V(s),
соответствующее t-й таблице. Если Vt(s) содержит более одного элемента: Vt(s) = {v1, v2, …, vk+2}, то в качестве производящей выбрать такую строку ![]() , что в последовательности множеств V1(s1), V2(s2), …, Vt(s) строка
, что в последовательности множеств V1(s1), V2(s2), …, Vt(s) строка ![]() появилась раньше (не
позднее) остальных
появилась раньше (не
позднее) остальных ![]() и затем сохранялась
вплоть до Vt(s); перейти к 2.
и затем сохранялась
вплоть до Vt(s); перейти к 2.
2.
Последовательно выбирать строку v, взятую в 1.,
до тех пор, пока ![]() . Как только
. Как только ![]() , вернуться к 1.
, вернуться к 1.
Подробнее об алгоритме можно прочитать в [2], стр. 344.
2.2.3. ТЕХНИКА ПОЛУЧЕНИЯ НАЧАЛЬНОГО ДОПУСТИМОГО БАЗИСАРешение каждым из приведенных выше методов может производиться только в том случае, если задача линейного программирования является или прямо, или двойственно допустимой. Такая допустимость означает наличие начального допустимого базиса в исходной задаче. Если задача допустима и прямо, и двойственно, то полученное решение – оптимально. В большинстве случаев после постановки задачи оказывается, что она не допустима ни прямо, ни двойственно. Поэтому приведем алгоритм получения начального допустимого базиса.
Пусть задача линейного программирования записана в канонической форме:
минимизировать
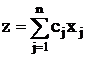
при условиях
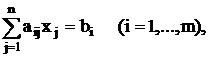
![]()
Все bi можно сделать неотрицательными, умножив, если надо, соответствующее
уравнение на –1. Тогда можно добавить в каждое уравнение искусственную
переменную ![]() (искусственные
переменные должны быть неотрицательными) таким образом, чтобы из искусственных
переменных образовать начальный базис:
(искусственные
переменные должны быть неотрицательными) таким образом, чтобы из искусственных
переменных образовать начальный базис:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Искусственные переменные можно получить из слабых переменных, используемых для превращения неравенств в уравнения. Действительно, если исходные ограничения задачи линейного программирования заданы в виде неравенств:
![]()
то, добавив слабую переменную в каждое неравенство, получим:
![]()
Если bi![]() 0, то si можно
использовать в качестве начальных базисных переменных.
0, то si можно
использовать в качестве начальных базисных переменных.
Различие между искусственными переменными ![]() и слабыми переменными si
состоит в следующем. В оптимальном решении задачи все искусственные переменные
должны быть равными нулю, поскольку в исходной задаче таких переменных нет. С
другой стороны, вполне возможно, что в оптимальном решении слабые переменные
будут иметь положительные значения. Для того, чтобы
искусственные переменные стали равными нулю, можно представить целевую функцию
следующим образом:
и слабыми переменными si
состоит в следующем. В оптимальном решении задачи все искусственные переменные
должны быть равными нулю, поскольку в исходной задаче таких переменных нет. С
другой стороны, вполне возможно, что в оптимальном решении слабые переменные
будут иметь положительные значения. Для того, чтобы
искусственные переменные стали равными нулю, можно представить целевую функцию
следующим образом:
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11


