 Дипломная работа: Разработка математической модели и ПО для задач составления расписания
Дипломная работа: Разработка математической модели и ПО для задач составления расписания
максимизировать
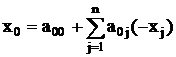
при условиях
![]()
![]()
|
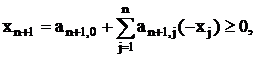
![]()
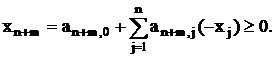
Условия (12) могут быть записаны как
|
![]()
Предположим, что для t=0 (т.е. для исходной
таблицы) все aij – целые и столбцы ![]() (j = 1 ,…, n) – лексикографически положительны. Тогда все столбцы на протяжении
вычислений остаются лексикографически положительными.
(j = 1 ,…, n) – лексикографически положительны. Тогда все столбцы на протяжении
вычислений остаются лексикографически положительными.
Прежде чем изложить способ получения дополнительного
ограничения из производящей строки, введем новое представление чисел. Пусть [x] обозначает
наибольшее целое число, не превосходящее x. Для любого числа y
(положительного или отрицательного) и положительного ![]() можно записать:
можно записать:
|
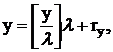
где ![]() (ry – неотрицательный остаток от деления нацело y на
(ry – неотрицательный остаток от деления нацело y на
![]() ). В частности,
). В частности, ![]() . Поэтому если
. Поэтому если ![]() , то
, то ![]() и r = 1. Если
и r = 1. Если ![]() , то
, то ![]() и r = 0.
и r = 0.
Вводимое дополнительное неравенство должно выполняться при любом целом решении задачи (12). Рассмотрим некоторое уравнение в t – таблице (опуская индекс строки) с a0
|
![]()
где x – соответствующая компонента вектора ![]() , а
, а ![]() - текущие небазисные
переменные. Можно выразить x, a0 и aj,
используя введенное выше представление (14):
- текущие небазисные
переменные. Можно выразить x, a0 и aj,
используя введенное выше представление (14):
|
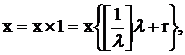
|
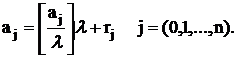
Подставив выражения (16) и (17) в (15) и переставив члены, получим:
|
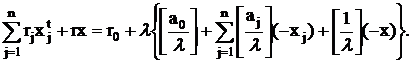
Поскольку ![]() ,
, ![]() и на переменные x и
и на переменные x и ![]() наложено требование
неотрицательности, левая часть уравнения (18) всегда неотрицательна. Рассмотрим
выражение в правой части, заключенное в фигурные скобки. Коэффициенты в этом
выражении представляют собой целые числа, а переменные подчинены требованию
целочисленности. Поэтому все выражение в скобках должно быть целым. Обозначим
его через s, т.е.:
наложено требование
неотрицательности, левая часть уравнения (18) всегда неотрицательна. Рассмотрим
выражение в правой части, заключенное в фигурные скобки. Коэффициенты в этом
выражении представляют собой целые числа, а переменные подчинены требованию
целочисленности. Поэтому все выражение в скобках должно быть целым. Обозначим
его через s, т.е.:
|
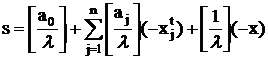 .
.
Целочисленная слабая переменная s является
неотрицательной. Действительно, если бы s было отрицательным, т.е.
принимало бы значения -1, -2, …, то
умножение на ![]()
![]() сделало
бы всю правую часть уравнения (18) отрицательной, в то время как левая часть
неотрицательна.
сделало
бы всю правую часть уравнения (18) отрицательной, в то время как левая часть
неотрицательна.
Рассмотрим два случая ![]() и
и ![]() . Для
. Для ![]()
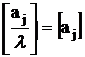 и
и 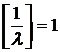 . Подставляя в уравнение (19) выражение для x из (15),
получим:
. Подставляя в уравнение (19) выражение для x из (15),
получим:
|
![]()
Полученное уравнение
есть не что иное как отсечение Гомори. Для ![]() имеем
имеем 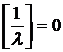 и уравнение (19)
приобретает вид:
и уравнение (19)
приобретает вид:
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11


