Дипломная работа: Разработка математической модели и ПО для задач составления расписания

(21)

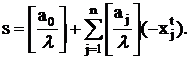
Уравнение (21) должно выполняться для любого целочисленного решения задачи (12). Заметим, что если a0 в уравнении (21). Потому уравнение (21) может использоваться в качестве ведущей строки в симплекс-методе. В частности, всегда можно выбрать достаточно большим, так чтобы ведущий элемент в строке (21) стал равным –1, что позволит сохранить целочисленность таблицы. Выбор соответствующего будет влиять на скорость сходимости алгоритма. Прежде всего опишем сам алгоритм. В качестве начального необходимо взять двойственно допустимое решение, которое можно получить добавлением ограничения xn+m+1=M – x1 - - … - xn 0, где M – достаточно большая константа, и проведением одной итерации с добавленной строкой и с лексикографически минимальным столбцом, взятыми в качестве ведущих. Алгоритм состоит из следующих шагов:

Шаг 0. Начать с двойственно допустимой матрицы A0 в уравнении (13), элементы которой – целые числа (матрица A0 может содержать и нецелые элементы, об этом см. [2], стр. 306).

Шаг 1. Среди строк с ai0i00 (i=1, …, n+m), то задача решена.)

Шаг 2. Выбрать (правило выбора будет описано дальше) и написать внизу таблицы дополнительную строку

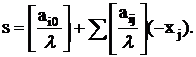
Эта строка выбирается в качестве ведущей.

Шаг 3. Провести шаг двойственного симплекс-метода, вычеркнуть дополнительную строку и вернуться к шагу 1.

Доказательство конечности алгоритма см. [2], стр. 303-304.

Правило выбора формулируется следующим образом.

Шаг 0. Пусть строка с номером v является производящей.

Шаг 1. Пусть - лексикографически минимальный столбец среди столбцов с avj

Шаг 2. Для каждого avj - наибольшее целое, такое, что 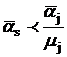(лексикографически меньше).

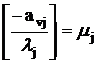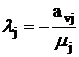Шаг 3. Пусть , а (строка v - производящая). Тогда

.

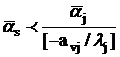Шаг 4. Положить для avj

Правило выбора , описанное выше, позволяет сделать ведущий элемент равным –1, при этом сохраняется двойственная допустимость таблицы и в то же время нулевой столбец будет максимально лексикографически уменьшаться.

Подробнее об алгоритме можно прочитать в [2], стр. 300.

2.2.2 Прямой алгоритм целочисленного программирования

Термин “прямой”, примененный к алгоритму целочисленного программирования, обозначает метод, который приводит к оптимальному решению посредством получения последовательно “улучшаемых” решений. Каждой из этих решений допустимо в том смысле, что оно удовлетворяет как линейным ограничениям, так и условию целочисленности. Одним из вероятных достоинств алгоритма является возможность прервать вычисления, до того как получено оптимальное решение, и использовать наилучшее из полученных решений как приближенное. Кроме того, можно использовать прямой алгоритм в соединении с двойственными алгоритмами, чтобы получать различные составные алгоритмы, которые могут переходить от фазы, дающей двойственно допустимые решения, к фазе, дающей прямо допустимые решения.

Естественным прецедентом для прямого алгоритма является полностью целочисленный алгоритм Гомори, поскольку в процессе этого алгоритма получается последовательность двойственно допустимых целочисленных решений. Следует напомнить, что полностью целочисленный алгоритм Гомори представляет собой модификацию двойственного симплекс-метода. Основное отличие этого алгоритма состоит в том, что в качестве ведущей строки используется отсечение Гомори с ведущим элементом, равным –1. Это отсечение получается из производящей строки, которая определяется как одна из возможных ведущих строк в двойственном симплекс-методе. Использование такого отсечения в качестве ведущей строки сохранит после итерации двойственную допустимость и целочисленность таблицы.

Оказывается, можно аналогично модифицировать симплекс-метод таким образом, чтобы получить алгоритм, который сохраняет прямую допустимость и целочисленность таблиц. Для описания вычислительной процедуры рассмотрим следующую задачу целочисленного программирования:

максимизировать

(22)

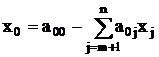
при условиях

,

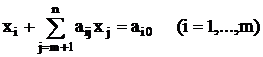(целые) (k=1,…,n),

где a0j, aij и ai0 – целые числа и ai00.

(23)

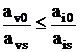Предположим, что столбец выбран в качестве ведущего и строка v – ведущая строка в итерации симплекс-метода, т.е. для всех строк I, в которых ais>0. Прежде чем провести процедуру исключения Гаусса в симплекс-методе, добавим к таблице отсечение Гомори, полученное из строки v:

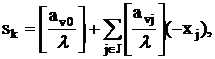
где J – множество индексов небазисных переменных в (22), sk – новая (базисная) слабая переменная и - неопределенная (временно) положительная константа.

Заметим, что если положить = avs, отсечение (23) будет обладать двумя важными свойствами. Во-первых,

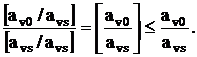
Это означает, что прямая допустимость таблицы сохраниться, если использовать отсечение (23) в качестве ведущей строки. Во-вторых, 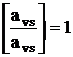, т.е. ведущий элемент равен 1 (если отсечение используется как ведущая строка). Легко удостовериться (путем исследования формул изменения базисных переменных), что преобразование симплексной таблицы с единичным ведущим элементом сохраняет целочисленность элементов симплексной таблицы.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11