Реферат: Исследование операций

Теперь составим таблицу выделения средств всем трем предприятиям. Так как N – общее количество составов равно 14, а максимально возможное количество составов для предприятий 1 и 2 =12, то всем трем предприятиям может быть выделено 13 или 14 составов. W3 – суммарная эффективность всех трех предприятий.

Количество      Составов	x3	x	Эффективность использования ресурсов
			q3	W2	W3
13	1	12	-458,52	4164,3	3705,78
	2	11	-597,94	3859,05	3261,11
	3	10	-642,36	3470,25	2827,89
	4	9	161,12	2555,55	2716,67
	5	8	201,4	2481,3	2682,7
14	2	12	-597,94	4161,3	3563,36
	3	11	-642,36	3859,05	3216,69
	4	10	161,12	3470,25	3631,12
	5	9	201,4	2555,55	2756,95
	6	8	1768,08	2481,3	4249,38

W3 максимальное равно 4249,38, следовательно Z = 4249,38.

x3 = 6; x2 = 2; x3 = 6.

Вывод:

В результате решения задачи динамического программирования я получил, что максимальное значение целевой функции Z =  = 4249,38 получается при количестве составов, выделенных 3 предприятиям N = 14, и количестве составов выделенных предприятию 3 x3 = 6. При этом количество составов для предприятий 1 и 2 равно 8. Максимальная эффективности использования 8 составов предприятиями 1 и 2 достигается при выделении предприятию 1 -  6 составов, а предприятию 2 – 2 состава, и она равна 2481,3. Следовательно x1 = 6, x2 = 2, x3 = 6, Z = 4249,38.

Плановые задания предприятиям:

, где P – плановое задание тыс. тонн, q – производительность состава, x – количество составов, i – номер предприятия.

Для предприятия 1:

тыс. тонн;

тыс. тонн;

тыс. тонн.

                           Графическая интерпретация решений.

1.    Решение задачи ЛП.

Из ограничения 1 задачи ЛП:

 

Выразим

Ограничения:

1)    x16,17 , значит 12 - x2  - x3  6,17;

x2 + x3  5,84

y1 = x2 + x3 = 5,84

x3 = 5,84 – x2;

2)    x2  6,18

y2 = x2 = 6,18;

3)    x3  5,66

y3 = x3 = 5,66;

4)    0,96 x1 + 0,12 x2 – 0,95 x3  0

0,96 (12 – x2 – x3) + 0,12 x2 – 0,95 x3  0

      -0,84 x2 – 1,9 x3 11,52

 0,84 x2 + 1,9 x3  11,52

 y4 = 0,84 x2 + 1,9 x3 = 11,52

 ;  

5)    –0,84 x1 + 1,06 x3  0

-0,84 (12 – x2 – x3) + 1,06 x3  0

0,84 x2 + 0,84 x3 + 1,06 x3  10,08

0,84 x2 + 1,9 x3 = 10,08

;

Целевая функция:

Z = 676,8 (12 – x2 – x3) + 459,25 x2 + 294,66 x3 = 8121,6 – 217,55 x2 – 382,14 x3;

Рассмотрим, что происходит с графиком целевой функции при ее увеличении:

1)    Z1 = 8000

8121,6 – 217,55 x2 – 382,14 x3 = 8000

-217,55 x2 – 382,14 x3 = 8000 – 8121,6

217,55 x2 + 382,14 x3 =121,6

;

X2	0	3
X3	0,32	-1,39

2)    Z2 = 9000

-217,55 x2 – 382,14 x3 = 9000 – 8121,6

217,55 x2 + 382,14 x3 =  – 878,4

x2	0	-3
x3	-2,3	-0,6

    Мы получили, что график функции Z2 расположен ниже чем график функции Z1. Однако Z2 > Z1 (9000 > 8000). Следовательно своего максимального значения целевая функция достигает в самой нижней точке области относительно целевой функции (в той точке, через которую график целевой функции будет проходить первым при уменьшении целевой функции). Обозначим эту точку на графике A. Координаты точки A (0,95;4,89). x2 = 0,95; x3 = 4,89, что соответствует решению с помощью симплекс – метода.

2.    Задача ЦЛП.

Максимального значения целевая функция задачи ЦЛП достигает при x2 = 1, x3 = 5. На графике решение задачи ЦЛП – точка B с координатами (1;5).

3.    Задача нелинейного программирования.

x2 = 0,17, x3 = 5,66. На графике точка C с координатами (0,17;5,66).

4.    Задача ДП.

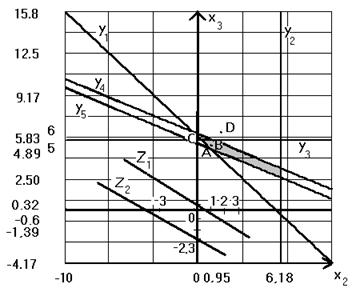x2 = 2, x3 = 6. На графике точка D с координатами (2;6). 

 Трудоемкость и эффективность решения модели различными методами.

Метод    Свойство	ЛП	ЦЛП	Нелинейное		ДП
Использование Симплекс – метода и ПК	Небольшое (1 проход)	Большое (много проходов)	Большое (много проходов)		НЕТ
Размер  расчетов без ПК	Низкий (только расчет плановых заданий)	Низкий (только расчет плановых заданий)	Средний (расчет дохода, прибыли, затрат, плановых заданий)		Большой (все расчеты производятся вручную)
Размер подготовительных  и промежуточных расчетов	Низкий (только ограничения)	Средний (ограничения ЛП + ветвление)		Высокий (ограничения ЛП + составление таблицы + промежуточ-ные подстановки коэффициен-тов)	Очень большой
Общее время решения	Низкое	Среднее		Среднее	Высокое
Чувствитель-ность к ограничениям по содержанию полезного компонента в руде	Есть	Есть		Есть	Нет
Использование коэффициента увеличения затрат при нагрузке	Нет	Нет		Есть	Есть
Размер целевой функции	Максимальный       6048,2412	Средний     5993,3501		Средний    5827,1611	Низкий       4249,38
Общая эффективность и приближенность условий к реальным	Низкая (не учитывается коэффициент изменения затрат и целочислен- ность решения)	Средняя (не учитывается коэффициент изменения затрат)		Средняя (не учитывается целочислен-ность решения)	Средняя (низкая прибыль)

 

                                                О проекте.

Проект выполнен студентом второго курса факультета РПМ Московского государственного горного университета Солодовниковым Дмитрием.

Использованная литература:

·     Резниченко С.С., Ашихмин А.А. Математические методы и моделирование в горной промышленности. – М.: Издательство Московского горного университета, 1997, 404 c.