 Реферат: Аппроксимация
Реферат: Аппроксимация
Кроме того первые k переменных двойственной задачи свободны, а остальные несвободны.
Целевая функция двойственной задачи
W= a1, n+1 u1 + a2, n+1 u2 + … + am, n+1 um + am+1, n+1
Совмещение в одной таблице прямой и двойственной задачи неслучайно. Решая прямую задачу, мы получаем о дновременно решение двойственной задачи, причем
max Z = min W = am+1, n+1
Сделаем замену переменных в таблице 1 , перебросив вспомогательную переменную yr на верх таблицы со знаком минус, а основную пременную xs на бок таблицы (ars¹0). Это означает движение из вершины x=(0, …, 0) в другую вершину многогранника W по его ребру. Элемент аrs называется разрешающим, строка r - разрешающей строкой, столбец s - разрешающим столбцом. Такая замена переменных носит название модифицированных жордановых исключений (МЖИ). Элементы матрицы а, не принадлежащие разрешающему столбцу или разрешающей строке, назовем рядовыми.
2.2 Описание исходных данных и результатов решения задачи линейного программирования.
Обсудим исходные данные (текстовой файл simp.dat) и результаты решения задачи линейного программирования (текстовой файл simp.res). В начале файла simp.dat расположены, так называемые, представительские данные - строковые данные, каждое из которых распологается в файле с новой строки:
1. Строка с номером варианта,
2. Строка с русским названием модуля,
3. Строка с координатами студента (ФИО, факультет, курс, группа),
4. Строка с датой исполнения.
Далее следуют строки файла с числовыми исходными данными:
1. Управляющий вектор kl - отдельная строка состоящая из трёх чисел kl1 , kl2 , kl3:
kl1=0, если необходимо получить решение только прямой задачи.
kl1=1, если необходимо получить решение только двойственной задачи.
kl1=2, если необходимо получить решение обеих задач.
kl2=0, если нет свободных переменных, иначе kl2 равен числу этих нуль-уравнений.
2. Число ограничений и переменных (отдельная строка ввода).
3. Коэффициенты расширенной матрицы a, начиная с отдельной строки ввода.
4. Вектор номеров свободных переменных, если они есть, начиная с отдельной строки ввода.
Результаты решения зависят от значения kl .
Если kl1=0, то при благоприятном исходе это будет вектор оптимального решения прямой задачи и оптимальное значение целевой функции. При неблагоприятном исходе, это одно из сообщений: либо "Система ограничений несовместна", либо "Целевая функция неограничена".
Если kl2=1, то же для двойственной задачи.
Если kl2=2, то сначала выдается решение прямой, а потом двойственной задачи. При не благоприятном исходе сообщения справедливы только для прямой задачи (для двойственной аналогичные сообщения не выдаются). Результаты помещаются в файл simp.res.
3.2 Описание модуля типов.
Для задания типов и файловых переменных вводного и выводного текстовых файлов используется модуль типов unit typesm, структура которого приведена ниже
unit typesm;
interface
const
mmax=20; nmax=20; e=1e-5;
type
klt =array[1..3] of integer;
at =array[1..mmax+1,1..nmax+1] of real;
vec1it =array[1..nmax] of integer;
vec2it =array[1..mmax] of integer;
vec1rt =array[1..nmax] of real;
vec2rt =array[1..mmax] of real;
var
fi, fo:text;
implementation
end.
В разделе констант заданы константы nmax и mmax, задающие максимальное число строк расширенной матрицы a без единицы, а также пороговая константа е, используемая в модуле поиска разрешающей строки. Константа е используется для обеспечения устойчивости алгоритма (модуль разрешающего элемента не должен быть слишком мал, а именно, больше е).
Ниже приведена таблица фактических и формальных параметров подпрограмм задач линейного программирования. Обозначения формальных и фактических параметров совпадают.
|
N/N |
Назначение |
Обозначение |
Тип |
| 1. | Управляющий вектор | k1 | ki1t |
| 2. | Число ограничений | m | integer |
| 3. | Число переменных | n | integer |
| 4. | Матрица коэффициентов | a | at |
| 5. | Вектор номеров свободных переменных | i1 | vec1it |
| 6. | Отслеживающий вектор основных переменных прямой задачи | p1 | vec1it |
| 7. | Отслеживающий вектор вспомогательных переменных двойственной задачи | q1 | vec1it |
| 8. | Отслеживающий вектор вспомогательных переменных прямой задачи | p2 | vec2it |
| 9. | Отслеживающий вектор основных переменных двойственной задачи | q2 | vec2it |
| 10. | Разрешающая строка | r | integer |
| 11. | Разрешающий столбец | s | integer |
| 12. | Вектор-решение прямой задачи | x | vec1rt |
| 13. | Вектор-решение двойственной задачи | u | vec2rt |
4.2 Укрупненная блок-схема задачи линейного программирования.
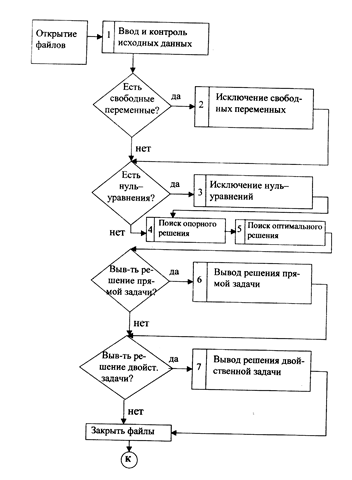
5.2 Параметры и заголовки процедур задачи линейного программирования.
В основной программе используются следующие переменные, которые описаны в разделе var:
m,n,r,s:integer;{числовые переменные целого типа}
Процедуры программы:
|
N/N |
Назначение |
Заголовок |
| 1. | Ввод и контроль исходных данных и вывод их в файл результатов | input(var k1:k1t; var m,n:integer; var a:at, var i1:vec1it; var p1,q1:vec1it; var p2,q2:vec2it) |
| 2. | Исключение свободных переменных | issp(var k1:k1t; m,n:integer; var a:at; var i1,p1,q1:vec1it; var p2,q2: vec2it) |
| 3. | Исключение нуль-уравнений | isnu(var k1:k1t; m,n:integer; var a:at; var p1,q1:vec1it; var p2,q2: vec2it) |
| 4. | Поиск опорного решения | opor(m,n:integer; var a:at; var p1,q1:vec1it; var p2,q2: vec2it) |
| 5. | Поиск оптимального решения | optim(m,n:integer; var a:at; var p1,q1:vec1it; var p2,q2: vec2it) |
| 6. | Вывод решения прямой задачи | outp(m,n:integer; var a:at; var p2: vec2it; x:vec1rt) |
| 7. | Вывод решения двойственной задачи | outd(m,n:integer; var a:at; var q1: vec1it; u:vec2rt) |
| 8. | МЖИ | mji ( m,n:integer; var a:at; r,s:integer) |
| 9. | Поиск разрешающей строки | nstro(m,n:integer; var a:at; r,s:integer var p2:vec2it) |
6.2 Блок-схема и параметры реализованной процедуры.
|
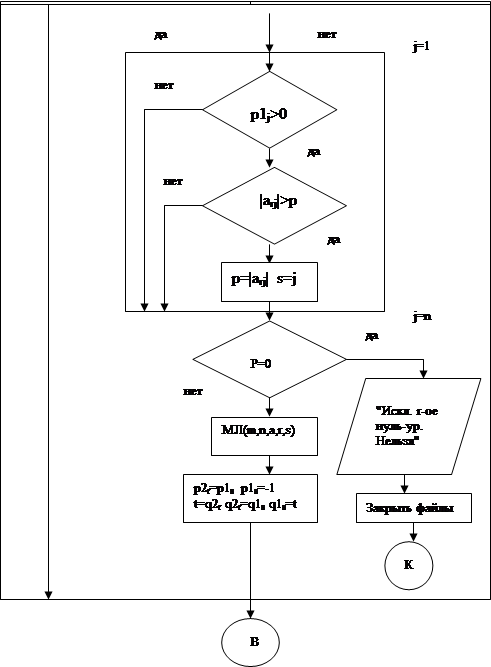 |
|||
|


