 Реферат: Аппроксимация
Реферат: Аппроксимация
Реферат: Аппроксимация
Министерство общего и профессионального образования Российской Федерации
Московский Государственный Строительный Университет
Кафедра информатики и прикладной математики
КУРСОВАЯ РАБОТА ПО ИНФОРМАТИКЕ
на темы:
1. Аппроксимация.
2. Разработка модуля исключения нуль-уравнений в комплексе “Решение задачи линейного программирования”.
Выполнил студент ЭОУС – I – 2: Моносов А. Л.
Преподаватель: доцент Марьямов А. Г.
Москва 1999.
Оглавление.
I. Математическая часть. Название…………………………………3.
1.1 Постановка задачи………………………………………………….3.
2.1 Изложение метода………………………………………………….4.
3.1 Блок-схема алгоритма. Описание исходных данных и результатов………………………………………………………………5.
4.1 Листинг программы, исходных данных и результатов……………6.
5.1 Список переменных основной программы………………………10.
6.1 Заголовки процедур и функций. Список их переменных……….10.
7.1 Ручной расчет……………………………………………………..11.
8.1 Обсуждение результатов с целью доказательства правильности алгоритма и программы………………………………………………..12.
9.1 Выводы…………………………………………………………….13.
II. Экономическая часть. Название………………………………..14.
1.2 Постановка задачи линейного программирования и задание на разработку модуля……………………………………………………...14.
2.2 Описание исходных данных и результатов решения задач линейного программирования………………………………………...18.
3.2 Описание модуля типов…………………………………………..19.
4.2 Укрупненная блок-схема задачи линейного программирования..20.
5.2 Параметры и заголовки процедур задачи линейного программирования……………………………………………………..21.
6.2 Блок-схема и параметры реализованной процедуры……………21.
7.2 Листинг модуля, исходных данных и результатов машинного расчета………………………………………………………………….23.
8.2 Ручной расчет задачи линейного программирования…………...24.
9.2 Выводы…………………………………………………………….26.
Список использованной литературы. ……………………………..27.
I. Математическая часть. Аппроксимация.
1.1 Постановка задачи.
Пусть величина y является функцией аргумента x. Это означает, что любому значению x из области определения поставлено в соответствии значение y. Вместе с тем на практике часто неизвестна явная связь между y и x, т.е. невозможно записать эту связь в виде y=f(x). В некоторых случаях даже при известной зависимости y=f(x) она настолько громоздка (например, содержит трудно вычисляемые выражения, сложные интегралы и т.п.), что ее использование в практических расчетах затруднительно.
Наиболее распространенным и практически важным случаем, когда вид связи между параметрами x и y неизвестен, является задание этой связи в виде некоторой таблицы {xi yi}. Это означает, что дискретному множеству значений аргумента {xi} поставлено в соответствие множество значений функции {yi} (i=0,1…n). Эти значения - либо результаты расчетов, либо экспериментальные данные. На практике нам могут понадобиться значение величины y и в других точках, отличных от узлов xi. Однако получить эти значения можно лишь путем очень сложных расчетов или провидением дорогостоящих экспериментов.
Таким образом, с точки зрения экономии времени и средств мы приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра y при любом значении (из некоторой области) определяющего параметра x, поскольку точная связь y=f(x) неизвестна.
Этой цели и служит задача о приближение (аппроксимации) функций: данную функцию f(x) требуется приближенно заменить (аппроксимировать) некоторой функцией g(x) так, чтобы отклонение (в некотором смысле) g(x) от f(x) в заданной области было минимальным. Функция g(x) при этом называется аппроксимирующей.
Для практики весьма важен случай аппроксимации функции многочленом:
g(x)=a0+a1x+a2x2+…+amxm (2.1)
При этом коэффициенты aj будут подбираться так, чтобы достичь наименьшего отклонения многочлена от данной функции.
Если приближение строиться на заданном множестве точек {xi}, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и др. При построении приближения на непрерывном множестве точек (например, на отрезке [a,b] аппроксимация называется непрерывной или интегральной).
2.1 Изложение метода (Точечная аппроксимация).
Одним из основных типов точечной аппроксимации является интерполирование. Оно состоит в следующем: для данной функции y=f(x) строим многочлен (2.1), принимающий в заданных точках xi те же значения yi, что и функция f(x), т.е. g(xi)=yi, i=0,1,…n.
При этом предполагается, что среди значений xi нет одинаковых, т.е. xi¹xk при этом i¹k. Точки xi называются узлами интерполяции, а многочлен g(x) - интерполяционным многочленом.
 |
|||||
|
|||||
Рис. 1
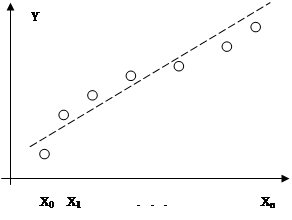
Таким образом, близость интерполяционного многочлена к заданной функции состоит в том, что их значения совпадают на заданной схеме точек (рис.1, сплошная линия).
Максимальная степень интерполяционного многочлена m=n; в этом случае говорят о глобальной интерполяции.
При большом количестве узлов интерполяции получается высокая степень многочлена (2.1) в случае глобальной интерполяции, т.е. когда нужно уметь один интерполяционный многочлен для всего интервала изменения аргумента. Кроме того, табличные данные могли быть получены путем измерений и содержать ошибки. Построение аппроксимируемого многочлена с условием обязательного прохождения его графика через эти экспериментальные точки означало бы тщательное повторение допущенных при измерениях ошибок. Выход из этого положения может быть найден выбором такого многочлена, график которого проходит близко от данных точек (рис.1, штриховая линия).
Одним из таких видов является среднеквадратичное приближение функции с помощью многочлена (2.1). При этом m £ n; случай m = n соответствует интерполяции. На практике стараются подобрать аппроксимирующий многочлен как можно меньшей степени (как правило, m=1, 2, 3).
Мерой отклонения многочлена g(x) от заданной функции f(x) на множестве точек (xi,yi) (i=0,1,…,n) при среднеквадратичном приближении является величина S, равная сумме квадратов разности между значениями многочлена и функции в данных точках:
n
S = å[g(xi)-yi]2
i=0
Для построения аппроксимирующего многочлена нужно подобрать коэффициенты a0, a1,…,am так, чтобы величина S была наименьшей. В этом состоит метод наименьших квадратов.
n
dS/da1=2å[ g(xi)-yi]2*1=0;
i=1
n
dS/da2=2å[ g(xi)-yi]2*xi=0;
i=1
…
n
dS/dam+1=2å[ g(xi)-yi]2*xim=0.
i=1
C A B
| n |
å xi |
… |
å xim |
a1 |
åyi |
||||
|
|
å xi2 |
… |
å xim+1 |
a2 |
åyixi |
||||
| … | …… | … | …… | … | … | ||||
|
å xim |


