Быстрый поиск

Курсовая работа: Комплексный анализ методов теории нечетких множеств

bi = ai n.

Значения ai и bi приведены в табл. 2.4.

Таблица 2.4

Собственный вектор матрицы полярных сравнений критериев и их весовые коэффициенты

Множество оптимальных альтернатив В с учетом различной важности критериев качества определяется путем пересечения нечетких множеств следующим образом:

Найдем множество оптимальных альтернатив с учетом полученных весовых критериев:

В = { min { 0,051,062; 0,70,318; 0,350,404; 0,250,589; 0,52,652; 1,00,972 }

min { 0,251,062; 1,00,318; 0,60,404; 0,70,589; 0,92,652; 0,750,972 }

min { 0,41,062; 0,30,318; 0,20,404; 0,30,589; 0,352,652; 0,60,972 }}.

Множество оптимальных вариантов В имеет вид:

Таким образом, лучшей альтернативой является банк а2 на втором месте банк a3 самым худшим вариантом для вклада денег является банк а1.

2. Выбор конкурентоспособного товара методом нечеткого отношения предпочтения

Проанализируем ряд виброзащитных технологий для выявления наиболее конкурентоспособной на определенном международном рынке.

Задачу выбора рационального виброизолятора с учетом наиболее важных критериев качества рассмотрим на примере анализа четырех альтернатив: а1 — пневматического виброизолятора; a2 — металлического торсионного элемента, работающего на скручивание; a3 — винтовой пружины; a4 — резинового элемента.

Для оценки альтернатив используем восемь критериев качества:

F1 — собственная частота колебаний виброизолятора (f, Гц);

F2—долговечность элемента (Т, лет);

F3 — габаритный размер (h, метр);

F4 — коэффициент передачи на резонансе (Tz, безразмерные единицы);

F5 — устойчивость к механическим повреждениям (шкала экспертных оценок);

F6 — стоимость (тыс. руб.);

F7 — шумоизоляция (дБ);

F8 — патентная чистота (условные единицы измерения).

На основании функций принадлежности всех альтернатив по восьми критериям определены их конкретные значения, которые представляют собой следующие нечеткие множества:

По этим данным составлены матрицы нечетких отношений предпочтения R1, ..., R8

Задача выбора решается в соответствии с описанной выше процедурой.

1. Строим нечеткое отношение Q1 = R1 Ç R2 Ç …Ç R8:

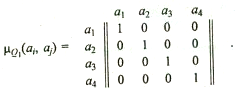
Находим подмножество недоминируемых альтернатив на множестве {А, }:

по всем i и j (i ¹ j):

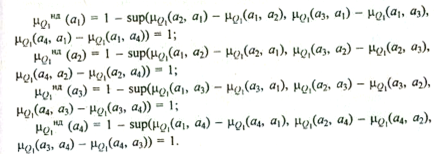
2. Строим отношение Q2.

Коэффициенты wk относительной важности критериев имеют следующие значения: w1 = 0,23, w2 = 0,09, w3 = 0,04, w4 = 0 23 w5 = 0,04, w6 = 0,09, w7 = 0,23, w8 = 0,04.

Определяем нечеткое отношение Q2.

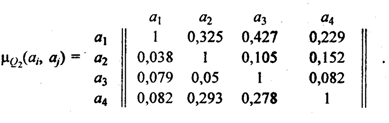
Находим подмножество недоминируемых альтернатив множества [А, }:

по всем i и j (i ¹ j):

3. Результирующее множество недоминируемых альтернатив есть пересечение множеств НД и НД

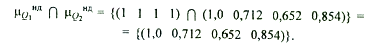
4. Следовательно, рациональным следует считать выбор альтернативы a1 имеющей максимальную степень недоминируемости.

3. Метод нечеткого логического вывода в задаче выбора фирмой кандидата на замещение вакантной должности бухгалтера

Руководство фирмы рассматривает кандидатов на замещение вакантной должности бухгалтера. Задача заключается в том, чтобы, используя описанный выше метод, выявить наилучшего претендента. Обсуждение среди членов руководства фирмы дало следующий результат:

d1: "Если кандидат имеет требуемые квалификацию, образование и опыт ведения бухгалтерского учета, то он — удовлетворяющий (отвечающий требованиям)";

d2: "Если он вдобавок к вышеописанным требованиям умеет работать с современным программным обеспечением (ПО), то он — более чем удовлетворяющий";

d3: "Если он дополнительно к условиям d2 обладает необходимыми юридическими знаниями, то он — безупречный";

d4: "Если он имеет все оговоренное в d3, кроме способности работать с современным ПО, то он — очень удовлетворяющий";

d5: "Если кандидат имеет необходимую квалификацию, имеет опыт ведения бухгалтерского учета, обладает юридическими знаниями, но не имеет высшего образования, он все же будет удовлетворяющим";

d6: "Если он не имеет квалификации и не имеет опыта ведения бухгалтерского учета, то он — неудовлетворяющий".

Анализ приведенных информационных фрагментов позволяет выявить шесть критериев, используемых для принятия решения:

Х1 — квалификация; Х2 — образование; Х3, — опыт ведения бухгалтерского учета; Х4, — умение работать с современным ПО; Х5 — юридическая грамотность, Y— удовлетворительность.

Для формулирования правил следует определить возможные значения лингвистических переменных Xi и Y, которые будут использоваться для оценки кандидатов:

d1: "Если Х1 = ПОДХОДЯЩЯЯ и X2 = ВЫСШЕЕ, и Х3 = ДОСТАТОЧНЫЙ. то Y = УДОВЛЕТВОРЯЮЩИЙ";

d2: "Если Х1 = ПОДХОДЯЩАЯ и X2 = ВЫСШЕЕ, и Х3 = ДОСТАТОЧНЫЙ, и X4 = СПОСОБЕН, то Y = БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ";

d3: "Если Х1 = ПОДХОДЯЩАЯ и Х2 = ВЫСШЕЕ, и X3 = ДОСТАТОЧНЫЙ, и Х4 = СПОСОБЕН, и X5 = ОБЛАДАЕТ, то Y = БЕЗУПРЕЧНЫЙ";

d4: "Если Х1 = ПОДХОДЯЩАЯ и Х2 = ВЫСШЕЕ, и Х3 = ДОСТАТОЧНЫЙ, и X4 = ОБЛАДАЕТ, то Y = ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ";

d5: "Если Х1 = ПОДХОДЯЩАЯ и X2 = НЕ ВЫСШЕЕ, и Х3 = ДОСТАТОЧНЫЙ, и X5 = ОБЛАДАЕТ, то Y = УДОВЛЕТВОРЯЮЩИЙ";

d6: "Если Х1 = НЕ ИМЕЕТ и Х3 = НЕДОСТАТОЧНЫЙ, то Y = НЕУДОВЛЕТВОРЯЮЩИЙ".

Переменная Y задана на множестве J = {0; 0,1; 0,2; ...; 1}.

Значения переменной Y заданы с помощью следующих функций принадлежности:

S = УДОВЛЕТВОРЯЮЩИЙ определено как mS(х) = х, х Î J;

MS = БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ — как mMS(x)=Öx; x Î J;

VS = ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ — как mVS(x) = х2, x Î J,

US = НЕУДОВЛЕТВОРЯЮЩИЙ — как mVS(x) = 1 - х, х Î J.

Выбор производится из пяти кандидатов на множестве U = {u1, и2, u3, u4, u5}.

В рассматриваемой задаче оценки кандидатов заданы следующими нечеткими множествами:

ПОДХОДЯЩАЯ (квалификация) А = {0,8/u1, 0,61u2, 0,5/u3, 0,1/u4, 0,3/u5};

ВЫСШЕЕ (образование) В = {0,5/u1,1/u2, 0/u3, 0,5/u4, 1/u5};

ДОСТАТОЧНЫЙ (опыт) С = {0,6/u1, 0,9/и2, 1/u3, 0,7/u4, 1/u5};

СПОСОБЕН (работать с ПО) D = {1/u1, 0,3/и2, 1/u3, 0/u4, 0/u5}',

ОБЛАДАЕТ (юридическими знаниями) Е = {0/u1, 0,5/u2, 1/u3, 0,8/u4, 1/u5}.

С учетом введенных обозначений правила d1, ...,d6 принимают вид:

d1 : “Если Х= А и В, и С, то Y =S”;

d2: "Если Х= А и В, и С, и D, то Y = MS":

d3: “Если X= А и В, и С, и D, и E, то Y = P”;

d4: “Если X = А и B, и С, и Е, то Y = VS”;

d5: “Если X = A, и не В, и С, и E, то Y = S”;

d6: “Если Х = не A и не С, то Y = US”.

Вычислим функции принадлежности для левых частей приведенных правил:

Теперь правила можно записать в виде:

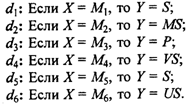
Используя для преобразования правил вида "Если Х = М, то Y = Q" импликацию Лукасевича mD(u, j) = min(l, 1-mM /(u) + mY (j)), для каждой пары (u, j) Î U х J получаем следующие нечеткие отношения на U ´ J:

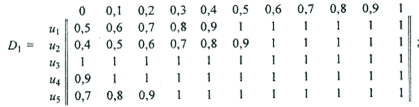
В результате пересечения отношений D1, ..., D6 получаем общее функциональное решение:

Для вычисления удовлетворительности каждой из альтернатив применим правило композиционного вывода в нечеткой среде:

Ek = Gk ° D, где Еk — степень удовлетворения альтернативы k;

Gk — отображение альтернативы k в виде нечеткого подмножества на U, D — общее функциональное решение. Тогда

Кроме того, в этом случае (u) = 0; u ¹ uk, (u) = 1; u = uk. Отсюда (i) = (uk, i) Другими словами, Еk есть k-я строка в матрице D. Теперь применим описанную выше процедуру для сравнения нечетких подмножеств в единичном интервале для получения наилучшего решения на основе точечных оценок.