Курсовая работа: Цифровая обработка сигналов

  D TT  D TT D TT  D TT 

  C  C  C  C

 a1(k) a2(k)  a3(k)  a4(k)

 ТАКТ

  M2

Рис. 2.5. Четырехканальный сигнатурный анализатор.

Она используется для анализа выходных реакций четырехвыходных цифровых схем. При этом конечное значение кода является результирующим значением сигнатуры S(y), представляющей собой компактную оценку сжатия четырех последовательностей

Можно показать, что схема, приведённая на рис.2.5, эквивалентна относительно конечного результата простейшей сигнатуры двухступенчатого сжатия информации (рис. 2.4). А это значит, что в обоих случаях для оценки эффективности можно применять формулу (2.3.3). Оба подхода получения сигнатур отличаются неравномерностью закона распределения вероятностей  необнаружения ошибки кратности m, а, следовательно, невысокой эффективностью. Кроме того, сигнатура многоканального сигнатурного анализатора (МСА), а также размерность сигнатуры S(y) однозначно определяется количеством выходов n исследуемой схемы. Поэтому с увеличением n сложность устройства сжатия и количество бит, используемых для представления сигнатуры S(y), принимает практически недопустимые размеры. Попытка использовать идею каскадирования многоканальных сигнатурных анализаторов позволяет уменьшить размерность результирующей сигнатуры, однако в этом случае оказывается сложным оценить достоверность такого анализатора [6], которая будет зависеть от организации взаимосвязи МСА и их конкретной реализации.

2.4.Многоканальный сигнатурный анализатор использованный в данной работе.

Предположим, что рассмотренный одноканальный анализатор используется для анализа цифрового узла, имеющего  каналов, причём  выходных последовательностей в данном случае преобразуются в одну последовательность вида

где  - значение двоичного символа на -м выходе цифрового узла в -й такт его работы, а тактовая частота работы анализатора в  раз выше частоты синхронизации исследуемого узла. При этом в каждый такт работы анализатора на его вход последовательно, начиная с первого выхода, поступают значения . Функционирование одноканального анализатора в многоканальном режиме, когда количество каналов равняется , описывается системой уравнений

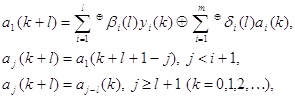
где численное значение коэффициентов  определяется на основании следующей системы уравнений

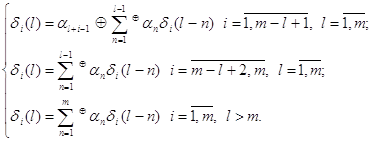
Коэффициенты определятся следующим образом:

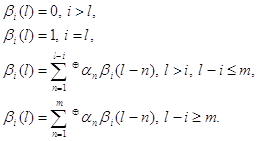
2.5. Алгоритм построения многоканального сигнатурного анализатора.

Для заданных значений  и , где определяет достоверность диагностирования, алгоритм построения многоканального сигнатурного анализатора состоит из следующих этапов.

1. Вычисляются постоянные коэффициенты

где

2. Определяются коэффициенты  причём значения коэффициентов  вычисляются на основании соответствующей системы уравнений, а значения остальных коэффициентов определяются согласно выражению

3. Строится функциональная схема многоканального сигнатурного анализатора на основании полученной системы уравнений

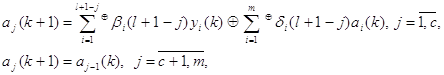
При этом используются результаты этапов 1 и 2, позволяющих однозначно определить топологию связей многовходовых сумматоров по модулю два, на выходах которых формируются значения .

2.6. Применение многоканальных анализаторов для диагностики неисправностей.

С помощью многоканальных сигнатурных анализаторов можно существенно ускорить процедуру контроля цифровых схем, которая практически увеличивается в n раз, где n – количество входов применяемого анализатора. В случае совпадения реально полученной сигнатуры с её эталонным значением считается, что с достаточно высокой вероятностью проверяемая цифровая схема находится в исправном состоянии. На этом процедура её исследования оканчивается. В противном случае, когда схема содержит неисправности, реальная сигнатура, как правило, отличается от эталонной, что служит основным аргументом для принятия гипотезы о неисправном состоянии схемы. В тоже время вид полученной сигнатуры не несёт никакой дополнительной информации о характере возникшей неисправности. Более того, остаётся открытым вопрос о том, какие из n анализируемых последовательностей, инициирующих реальную сигнатуру, содержат ошибки, т.е. возникает задача локализации неисправности с точностью до последовательности, несущей информацию о её присутствии. Рассмотрим возможные варианты решения данной задачи для случая применения n – канальных анализаторов.

Предварительно докажем следующую теорему.

Теорема. Суммарная сигнатура S(x), полученная для последовательностей  на n – канальном сигнатурном анализаторе, равна поразрядной сумме по модулю два сигнатур , , причём каждая из сигнатур , формируется для последовательности  при условии, что .

Доказательство. В n – канальном анализаторе n входных последовательностей преобразуются в одну вида:

Такая входная последовательность, анализируемая n канальным сигнатурным анализатором, описывается следующим двоичным полиномом:

 , (2.6.1)

который состоит из суммы по модулю два полиномов вида:

 , (2.6.2)

описывающих выходные последовательности . Каждый полином  можно представить в виде соотношения:

 , (2.6.3)

где -полином, взаимно обратный полиному , используемому для реализации n – канального сигнатурного анализатора; - сигнатура последовательности .

Просуммировав по модулю два правые и левые части равенства (2.6.3), получим, что полином  будет определяться как

 (2.6.4)

для которого также справедливо соотношение , т.е.

 (2.6.5)

В результате сравнения двух последних равенств можно заключить, что суммарная сигнатура S(x), полученная для последовательностей  равна поразрядной сумме по модулю два сигнатур  каждой из входных последовательностей:

  (2.6.6)

что и требовалось доказать.

Основной результат данной теоремы, выраженный соотношением (2.6.5), справедлив для примитивного полинома  и произвольных значений n и l. Следствием этой теоремы является возможность определения эталонной сигнатуры для произвольного множества входных последовательностей. Так, эталонное значение сигнатуры для первой, второй и пятой последовательностей будет вычисляться как

 

Используя результаты теоремы, можно формализовать процедуру контроля цифровой схемы. При этом входными последовательностями  этого анализатора в общем случае могут быть последовательности, формируемые на входных, промежуточных и выходных полюсах схемы, для которых в результате предварительных исследований определены значения эталонных сигнатур . Не нарушая общности, предположим, что n=2d, и представим процедуру контроля в виде следующего алгоритма.

Алгоритм контроля цифровой схемы локализацией неисправности до первой последовательности, содержащей вызванные ею ошибки.

В результате анализа n=2d реальных последовательностей  на n – канальном анализаторе определяется значение сигнатуры S*(x), которое соответствует соотношению:

По выражению

 

вычисляется эталонное значение сигнатуры S(x).

Реальное значение сигнатуры S*(x) сравнивается с эталонной сигнатурой S(x). В случае выполнения равенства S*(x) и S(x) считается процедура диагностики оконченной. В противном случае, когда S*(x)¹S(x) выполняется следующий этап алгоритма.

Все множество входных последовательностей разбивается на две группы, причём номера последовательностей  составляют множество А1={1,2,3…n/2}, а номера последовательностей  составляют множество А2={n/2+1,n/2+2,…n}. Значению i присваивается значение 1.

В результате анализа реальных последовательностей, номера которых задаются множеством А1 на n – канальном сигнатурном анализаторе при условии, что последовательности, номера которых определяет множество А2, являются нулевыми, определяется значение реальной сигнатуры.

На основании выражения

 

определяем S(x).

Проверяется справедливость равенства S*(x)=S(x), в случае выполнения множество А1 заменяется элементами множества А2.

Значение переменной i увеличивается на 1 и сравнивается с величиной n, если i<n, то совершают вышеприведённые действия с элементами множества А2.

Единственный элемент множества А1 представляет собой номер ошибочной последовательности.

Процедура контроля цифровой схемы считается законченной.

2.7. Оценка достоверности многоканального сигнатурного анализатора.

Учитывая эквивалентность функционирования n - канального сигнатурного анализатора и соответствующего ему одноканального анализатора относительно результата сжатия n входных последовательностей  логично оценить достоверность МСА, используя результаты, полученные для одноканального сигнатурного анализатора. Действительно, в случае применения примитивного полинома вероятность необнаружения ошибок в последовательностях  многоканальным сигнатурным анализатором для  где m – старшая степень порождающего полинома, будет определяться соотношением:

Это соотношение справедливо для любого соотношения  и , произведение которых равно 2m-1.[6] Приведённая интегральная характеристика эффективности МСА, также как и характеристика одноканального сигнатурного анализатора, является достаточно приближённой оценкой, справедливой для общих допущений. Более полной характеристикой МСА будет распределение вероятностей  необнаружения возникшей ошибки кратности m в анализируемых последовательностях . При этом численное значение указанных вероятностей, как и в случае одноканального анализатора, определяется выражениями:

Попытка применить это выражение для оценки значений  при анализе последовательности , когда  на n – канальном анализаторе не всегда позволяет получить верные результаты.

Теорема. Множество ошибок последовательности  необнаруживаемых одноканальным СА, реализованном на основании примитивного полинома , старшая степень которого равна m, соответствует множеству необнаруживаемых ошибок n = 2d – канальным анализатором, (d – целое положительное число) при условии отсутствия ошибок в последовательностях .

Таким образом, достоверность многоканального сигнатурного анализатора может быть оценена либо интегральной величиной , либо распределением вероятностей  необнаружения m - кратной ошибки в анализируемых последовательностях . Более предпочтительным значением n является значение, удовлетворяющее требованию n = 2d. Анализ последовательности  для  на подобном анализаторе будет эквивалентен анализу на соответствующем одноканальном анализаторе.