 Курсовая работа: Цифровая обработка сигналов
Курсовая работа: Цифровая обработка сигналов
Сдвиг Старт Стоп
Рис.2.3. Структурная схема сигнатурного анализатора.
меньше
величины 2m-1 и соответственно определяет длину
сжимаемой последовательности. По истечении ![]() тактов функционирования сигнатурного анализатора на его элементах
памяти фиксируется двоичный код, который представляет собой сигнатуру,
отображаемую в виде 16-ричного кода.
тактов функционирования сигнатурного анализатора на его элементах
памяти фиксируется двоичный код, который представляет собой сигнатуру,
отображаемую в виде 16-ричного кода.
Таким образом, путём формирования тестовой последовательности на входах анализируемого цифрового устройства для каждого его полюса находим эталонные значения сигнатур, множество которых запоминается и в дальнейшем используется для сравнения со значениями сигнатур, снимаемых с проверяемых устройств. Любое отличие реально полученной сигнатуры от эталонной свидетельствует о том, что полюс схемы функционирует отлично от случая исправного состояния устройства. Причина, вызвавшая отличие сигнатур на данном полюсе, может быть установлена последовательным анализом сигнатур от указанного полюса к входам устройства.
Эффективность использования такого сигнатурного анализатора ограничивается наличием в нём только одного информационного входа, в то время как количество выходов сложных цифровых узлов достигает значительных величин. Исследование подобных узлов осуществляется с использованием нескольких сигнатурных анализаторов, путём свёртки по модулю два выходных последовательностей или с применением некоторых других схемных решений.[1] Применение таких подходов для анализа многовыходных цифровых схем приводит или к существенному увеличению аппаратурных затрат, или к уменьшению величины вероятности P обнаружения ошибки. Поэтому для многовыходных цифровых узлов создание высокоэффективных цифровых анализаторов весьма актуально.
2.3. Многоканальные сигнатурные анализаторы.
Проблема
анализа многовыходных цифровых схем и процесс их тестирования заключается в определении
возникновения неисправности схемы по её выходным реакциям. Отличительной
особенностью подобного анализа является необходимость исследования достаточно
большого количества выходных реакций схемы (число их может достигать нескольких
сотен). Поэтому использование традиционных методов компактного тестирования,
применяемых для одновыходных цифровых схем, в данном случае не позволяет
получить желаемого эффекта.[5] Действительно, попытка провести анализ n - выходной цифровой схемы одноканальным СА приводит к
увеличению в n раз времени, необходимого для анализа
схемы, или оборудования, требуемого для реализации n сигнатурных анализаторов. При этом остаётся открытым вопрос о
разрядности сигнатуры, которая также может увеличиться в n раз. Поэтому на практике чаще всего используют специальные
методы и приёмы. Наиболее часто применяемым из них является метод, основанный
на преобразовании n выходных последовательностей ![]() длиной
длиной ![]() в одну последовательность
в одну последовательность
![]() по
выражению:
по
выражению:
![]() (2.3.1)
(2.3.1)
Практическая реализация этого метода может быть выполнена как процедура сжатия в пространстве или во времени. В том и другом случае реализуется идея получения компактных оценок, характерная для методов компактного тестирования.
Как показано в [6] эффективность алгоритма сжатия информации, реализующего соотношение (2.3.1) определяется как:
![]() (2.3.2)
(2.3.2)
где
m - кратность ошибки, причём для нечётных
значений m ![]() (
(![]() - это вероятность необнаружения
ошибки кратности m).
- это вероятность необнаружения
ошибки кратности m).
Для
оценки вида распределения вероятностей ![]() рассмотрим конкретный пример n=3 – выходной цифровой схемы, длина
рассмотрим конкретный пример n=3 – выходной цифровой схемы, длина ![]() выходных реакций которой составляет
21. В результате преобразования трех исходных последовательностей
выходных реакций которой составляет
21. В результате преобразования трех исходных последовательностей ![]() в
последовательность
в
последовательность ![]() , некоторые их ошибки станут
необнаруживаемыми и будут оцениваться выражением:
, некоторые их ошибки станут
необнаруживаемыми и будут оцениваться выражением:
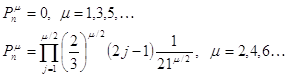 (2.3.3)
(2.3.3)
которое
справедливо для ![]() .
.
Ограничиваясь
![]() , определяем
согласно (2.3.3)
, определяем
согласно (2.3.3) ![]() .
.
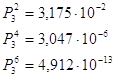
Анализ
полученных численных значений вероятностей ![]() , а также общего выражения (2.3.2)
показывает неравномерность закона их распределения, что свидетельствует о
достаточно невысокой эффективности рассматриваемого алгоритма сжатия. Кроме
того, необходимо отметить большую размерность результата сжатия, которая равна
длине
, а также общего выражения (2.3.2)
показывает неравномерность закона их распределения, что свидетельствует о
достаточно невысокой эффективности рассматриваемого алгоритма сжатия. Кроме
того, необходимо отметить большую размерность результата сжатия, которая равна
длине ![]() выходных
реакций схемы. Поэтому на практике чаще всего используется компромиссное
решение, заключающееся в двухступенчатом преобразовании выходных реакций n – выходной цифровой схемы. Первоначально n выходных последовательностей
выходных
реакций схемы. Поэтому на практике чаще всего используется компромиссное
решение, заключающееся в двухступенчатом преобразовании выходных реакций n – выходной цифровой схемы. Первоначально n выходных последовательностей ![]() длиной
длиной ![]() преобразуются в последовательность
преобразуются в последовательность ![]() по выражению
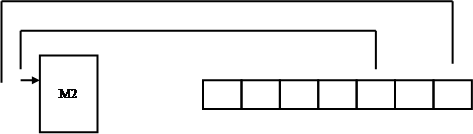
(2.3.1). Далее сформированная таким образом последовательность
по выражению
(2.3.1). Далее сформированная таким образом последовательность ![]() снимается в m – разрядную сигнатуру (рис. 2.4)
снимается в m – разрядную сигнатуру (рис. 2.4)
![]()
![]()

|
![]() Y2(k)
Y2(k)
Y0(k) S(x)
![]() Yn(k)
Yn(k)
Рис. 2.4. Многоканальный сигнатурный анализатор.
Эффективность данного преобразования согласно [6] при m=4 определится как
![]() (2.3.4)
(2.3.4)
где m – старшая степень порождающего полинома.
Эта
формула справедлива, когда ![]() .
.
Наиболее
распространенная структура многоканального сигнатурного анализатора для
исследования многовыходных цифровых схем, которая построена на базе
порождающего полинома ![]() , приведена на рис. 2.5.
, приведена на рис. 2.5.
![]()
![]()
![]()
![]() j1(k) j2(k) j3(k) j4(k)
j1(k) j2(k) j3(k) j4(k)




M2 M2 M2 M2


