Быстрый поиск

Реферат: Курс микроэкономики

– оптимальный потребительский набор, который мы находим.

– совокупный спрос по товару j.

Сопоставим совокупный спрос и совокупное предложение. Каждый потребитель должен прийти к состоянию равновесия и при этом должно соблюдаться макроэкономическое равновесие. Если это не выполняется, то возникают вопросы:

1. Существует ли равновесная система?

2. Можно ли к ней прийти?

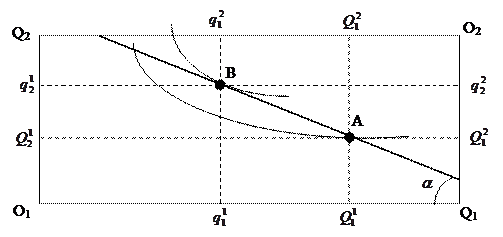Рассмотрим процесс торговли. Торговля – сделка между участниками системы, эквивалентная по стоимости. Рассмотрим экономику, состоящую из двух участников и двух товаров. Точка А – начальная. Цены известны.

Это ящик Эджуорта.

(1) ; все возможные эквивалентные сделки лежат на бюджетной линии. Предположим, что В – желаемая точка. Переход от А к В сопровождается повышением полезности для первого участника.

Экономический смысл торговли: торговля – это эквивалентная сделка, которая ведет к повышению полезности.

(2)

– условие эквивалентного обмена.

Для случая многих товаров выполняется следующее:

– закон Вальраса

Для любой начальной точки если выполняется условие Вальраса, то потребитель остается на той же Rk, т.е. все заключенные им сделки эквивалентны.

Точка В является оптимальным потребительским набором только для определенной системы цен.

Найти все оптимальные потребительские наборы для любой системы цен. Это ГМТ всех точек равновесия, полученных для различных систем цен при условии эквивалентного обмена.

Рассмотрим положение 2–ого участника:

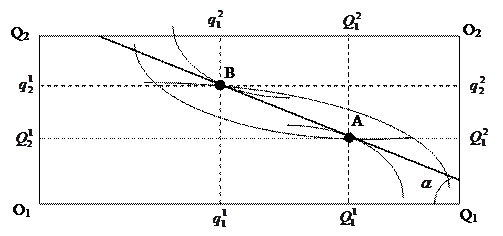
R1 = R2, т.е. бюджетные линии участников совпадают. Это означает, что когда второй продает все, что у него имеется, он может купить все, что есть у первого. Любые эквивалентные сделки 2–ого участника лежат на R2.

Существует ли такая система цен, при которой торговля является абсолютно взаимовыгодной?

Найдем контрактную линию 2–ого участника. DG – контрактная линия. Совместим контрактные линии обеих участников.

Существует единственная система цен, которая позволяет осуществлять такую эквивалентную сделку, при которой оба участника переходят к состоянию равновесия.

Если соотношение цен равно j, то оба участника в одинаковой степени заинтересованы в переходе от А к Е, т.е. в совершении эквивалентной сделки, что дает им совместную максимизацию полезности.

Итак, мы выяснили:

· Экономический смысл торговли;

· Что торговля осуществляется при ориентации на контрактные линии;

· Что существует единственная система цен, при которой торговля является взаимовыгодной.

Вернемся к описанию экономической системы. Будет ли действовать экономическая система в направлении установления равновесных цен? Используем модифицированную схему голландского аукциона:

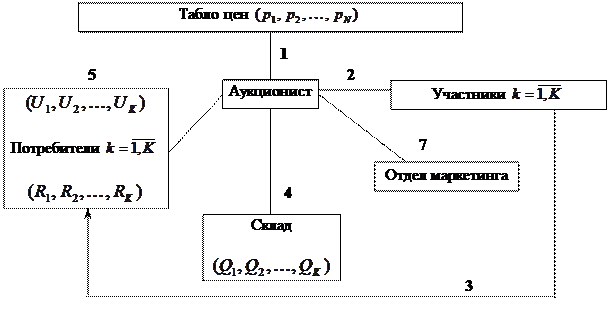
Этапы:

1. Аукционист устанавливает любую начальную систему цен.

2. Участники системы смотрят на систему цен и определяют свои бюджеты:.

3. Рассчитав Rk, участники превращаются в потребителей.

4. Участники свои товары передают Аукционисту, который отправляет их на склад. Аукционист отдает участникам деньги (чеки, расписки) на сумму RK каждому потребителю. Аукционист выступает в виде центра, осуществляющего эмиссию денег в системе.

5. Потребители решают свои потребительские задачи, находя оптимальный спрос .

6. Потребители обращаются к Аукционисту, предъявляя платежеспособный спрос на необходимые им товары.

7. Аукционист сопоставляет совокупные спрос и предложение и сопоставляет выпущенные чеки и платежеспособный спрос в денежной форме. Теперь должны сойтись два баланса – натуральный и денежный. Если балансы не соблюдаются, то Аукционист пересчитывает цены до тех пор, пока не сойдётся баланс.

Если функции потребления неоклассические, то соответствующая задача имеет решение и она единственная. Это означает, что в экономике торговли существует равновесная система. При этой системе участники могут заключить такие эквивалентные сделки, что:

· Они все будут находиться в состоянии равновесия;

· Совокупный спрос будет равен совокупному предложению;

· Все выданные чеки будут полностью погашены.

Будет ли экономическая система в отсутствии аукциониста стремится к равновесию? Если действия участников рациональны, то они фактически будут повторять действия аукциониста. В виде фигуры аукциониста на самом деле мы видим олицетворение действия механизма законов спроса и предложения.

6

Модель дает нам большое представление о роли денег в экономике. Мы до сих пор вели речь о реальном секторе. Деньги играют роль посредника и эталона ценностей, сами по себе реальной ценностью не являясь. Количество денег, необходимое данной системе зависит от товарных цен и массы товаров. При увеличении и того, и другого необходимо пропорциональное увеличение денежной массы. Это простая количественная версия теории денег.

Глава 2:Полная модель Вальраса

№1. ЭКОНОМИКА ПРОИЗВОДСТВА.

Мы рассмотрим еще один случай частного равновесия, но в рассмотрение включим процесс производства.

Условие задачи:

Рассмотрим экономическую систему, в которой присутствует множество потребителей и множество фирм. Объединим всех потребителей и все фирмы в 2 группы и будем представлять, что в экономике есть 2 потребителя и 2 фирмы. У каждого из потребителей есть свои функции предпочтения (U1, U2). Пусть в системе присутствуют 2 ресурса, которыми владеют потребители (L, K). L~1/2 – количество труда, которым обладает потребитель 1 или 2. L~ – сумма труда. То же самое с K~1/2, K~. L~, K~ –– максимальное совокупное предложение факторов.

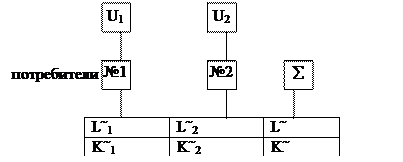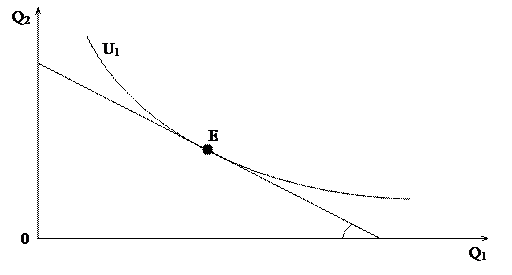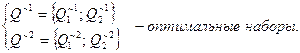
Зная наборы, мы можем просуммировать продукты: .

Рассмотрим фирмы:

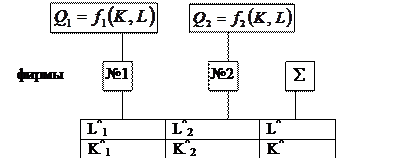
В начальном состоянии цены неизвестны.

Предположим, что цены известны:

– максимальный бюджет первого потребителя.

– максимальный бюджет второго потребителя.

Максимальный бюджет получается в том случае, если потребитель сумеет продать все свои ресурсы.

(*) – максимальный совокупный факторный доход.

– сумма бюджетов. Эта величина равна максимальной величине потребительских расходов.

Предположим, каждый из потребителей решил свою стандартную задачу, полностью израсходовал бюджет и оказался в равновесии. В этом случае потребительские расходы распишутся так:

(**) – суммарные потребительские расходы, если потребители сумели приобрести нужные им товары в нужном количестве.

Если уравнение (*) равно уравнению (**), то суммарный факторный доход равен суммарным потребительским расходам.

Насколько обеспечено потребление со стороны производства? Т.е. покупательский спрос должен найти соответствующее ему предложение со стороны фирм. Предложение факторов должно найти соответствующий спрос со стороны производства.

Будет ли поддерживаться баланс между сферой производства и сферой потребления?

Решение задачи:

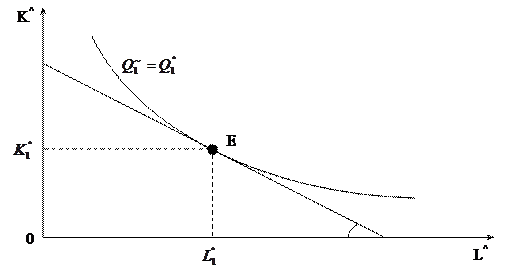Есть 2 пути анализа: