Реферат: Проектирование и исследование механизмов двигателя внутреннего сгорания

  .

1). Радиусы делительных окружностей:

2). Радиусы основных окружностей:

Расчётные коэффициенты смещения х1 и х2 для рассчитываемой передачи должны прежде всего обеспечивать отсутствие подреза (хmin) и заострения зубьев (хmax), а также гарантировать минимально допустимую величину коэффициента перекрытия. Следовательно, должно соблюдаться условие хtmin<x1,2<xmax.

3). Минимальное число зубьев на нулевом колесе, которое можно нарезать без подреза:

4). Минимальные коэффициенты смещения:

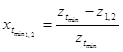
Максимальный коэффициенты смещения не может быть определён непосредственно, отсутствие заострения может быть выявлено после подсчёта толщины зуба по окружности вершин и удовлетворено при условии: .

5). Выбор коэффициента смещения:

Коэффициент смещения х2 выбирается по ГОСТ-18532-83.

6). Угол зацепления передачи:

Решается с помощью подпрограммы RIMT

7). Коэффициент воспринимаемого смещения:

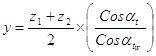
8). Коэффициент уравнительного смещения:

9). Радиусы делительных окружностей:

10). Межосевое расстояние передачи:

11). Радиусы окружностей вершин:

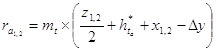
12). Радиусы окружностей вершин:

13). Высота зубьев колёс:

14). Толщина зубьев по дугам делительных окружностей:

15). Углы профиля на окружностях вершин зубьев колёс:

16). Толщина зубьев на окружностях вершин зубьев колёс:

Качественные показатели передачи.

1). Коэффициент перекрытия зубчатой передачи:

, где

,

2). Коэффициент скольжения:

   

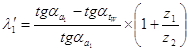
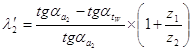
3.1.4 Анализ результатов расчёта на ЭВМ.

Для построения картины зубчатого зацепления необходимо выбрать значения параметров зубчатого зацепления, приведенные на стр. 19 в распечатке расчётов на ЭВМ. Для этого нужно определить величину х1 – расчётного коэффициента смещения.

3.2  Построение геометрической картины эвольвентного зубчатого зацепления.

3.2.1 Откладываем межосевое расстояние аW=O1O2 – сумму радиусов начальных окружностей.

3.2.2 Проводим радиусы выступов (ra1, ra2), ножек (rf1, rf2), основных (rb1, rb2) и делительных (r1, r2) окружностей.

3.2.3 Проверяем радиальный зазор с=с*´m, где с*=0,25.

3.2.4 Проводим радиусы основных окружностей и отмечаем на них точки N1 и N2, O1N1 расположится под углом к O1O2 - aWt=25° 04'01", O2N2 - aWt=25° 04'01".

3.2.5 Через точки N1 и N2 проводим общую касательную к окружностям rb1 и rb2. N1N2 – есть теоретическая линия зацепления.

3.2.6 Расстояние N1Р по теоретической линии зацепления N1N2 делим на 4 равные части. Такие же отрезки откладываем за точку N1 и получаем точки 1-6.

3.2.7 Из точки 3 раствором циркуля "3-Р" делаем на rb1 засечку – точка q. Дугу основной окружности rb1 – qN1 делим на 4 равные части и продолжаем деления за точку N1, получаем точки 1,2,3,4,5.

3.2.8 Точки на основной окружности соединяем с центром вращения шестерни.

3.2.9 Перпендикулярно радиусам проводим касательные к основной окружности в каждой точке.

3.2.10 Замеряем расстояние по теоретической линии зацепления: 1Р, 2Р, …, 6Р и из точек 1', 2', …, 6' делаем засечки на соответствующих касательных.

3.2.11 Соединяем полученные точки на касательных, получаем эвольвенту 1-го колеса.

3.2.12 Строим ножку зуба. Для  этого точку q соединяем с центром вращения 1-го колеса и радиусом rf=0,38´m делаем скругления.

3.2.13 Отложив толщину зуба по дуге делительной окружности S1, строим левый профиль зуба. Разделив толщину зуба пополам, получаем ось симметрии зуба.

3.2.14 Отложив шаги Рt на хорде делительной окружности влево и вправо, получаем оси 2-го и 3-го зубьев и строим три зуба второго колеса.

3.2.15 Определяем длины активной линии зацепления АВ. Расстояния по теоретической линии зацепления N1N2 между точками пересечения окружностей выступов каждого колеса с теоретической линией зацепления – есть практическая линия зацепления.

3.2.16 Определяем дуги зацепления. Через точки теоретической линией зацепления Н1 и Н2 проводим  правый профиль зуба первого колеса и левый профиль второго колеса.

3.2.17 Определяем рабочие части боковых профилей зубьев. Радиусами О1Н2 иО2Н1 проводим дуги до пересечения с боковыми профилями зубьев.

3.3 Синтез планетарного редуктора.

3.3.1 Выбор числа зубьев методом обращения движения.

  Þ 

принимаем z4=40, тогда z6=2,8´40=112>85 – целое число. Число z5 определяем из условия соседства: >17 – целое число.

3.3.2 Проверка условия сборки.

Приняв z4=40, z5=36, z6=112, проверяем передачу на условие сборки без натягов (при k=4; p=0):

 – целое число, условие соблюдается.

3.3.3. Определение размеров планетарного редуктора.

, откуда

d4=m´z4=8´40=320 мм

d5=m´z5=8´36=288 мм

d6=m´z6=8´112=896 мм

3.3.4 Графическое построение редуктора, планов линейных и угловых скоростей.

Вычерчиваем полученный механизм в масштабе ml=0,0064 м/мм и на вертикальную прямую сносим все характерные точки.

w4=w1=209,44 рад/с., тогда vА=w1´r4=209,44´0,16=33,51 м/с. Строим картину линейных скоростей с масштабным коэффициентом mv=vА/lvА=33,51 (м/с)/44 (мм)=0,7616 м/с/мм. Определяем скорости точек по картине линейных скоростей:

vC=0

vO=0

vB=lvВ´mv=32 (мм)´ 0,7616 (м/с/мм)= 24,37 м/с.

Для построения плана угловых скоростей откладываем отрезок ОО и из нижнего его конца проводим лучи, параллельные картинам скоростей звеньев. Угловые скорости изображены с масштабным коэффициентом , а

рад/с, по построению - w4= lw4´mw=75´2,7294=204,71 рад/с;

 рад/с, по построению - w4= lw4´mw=20´2,7294=54,59 рад/с;

 рад/с, по построению - w4= lw4´mw=75´2,7294=119 рад/с;

 

4 Синтез кулачкового механизма.

4.1 Задача синтеза кулачкового механизма.

Задача синтеза кулачкового механизма состоит в том, чтобы построить профиль кулачковой шайбы, удовлетворяющей заданным требованиям.

1). Закон движения толкателя.

2). Угловая скорость кулачка.

3). Рабочий угол профиля jр=120°.

4). Перемещение толкателя h=12 мм.

5). Отношение максимального ускорения толкателя к минимальному  .

4.2 Построение диаграммы аналогов ускорений.

4.3 Построение диаграммы аналогов скоростей и перемещения толкателя методом графического интегрирования.

Масштабные коэффициенты:

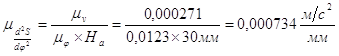
4.4 Определение минимального радиуса кулачка.

При определении минимального радиуса кулачка с поступательно движущимся толкателем строится диаграмма зависимости перемещения от аналога скоростей S=f(), причём . По вертикальной оси откладываем S, а по горизонтальной - . На пересечении соответствующих прямых получим точки, соединяем их и проводим прямую под углом aдоп.=45° к горизонтальной оси. На пересечении с осью S получаем точку О – расстояние от неё до горизонтальной оси и есть минимальный радиус кулачка, он равен rmin=ОА´m=105´0,0004= =0,042 м, принимаем rк=0,045 м.

4.5 Профилирование кулачка.

При графическом методе построения кривой профиля кулачка используют метод обращения движения: кулачок на чертеже считают неподвижным, а стойку – вращающейся с угловой скоростью (-w11).

Строим положение механизма с масштабным коэффициентом ml=0,0005 м/мм.

Проводим окружность радиусом rк, угол рабочего профиля, который делим на 17 частей – углы, величина которых определяется по диаграмме аналогов ускорений. Продолжаем прямые, делящие угол рабочего профиля, и откладываем на них от радиуса величину хода толкателя. Соединяя точки линией, получаем профиль кулачка.

Список  использованной литературы:

1). Артоболевский И.И. "Теория механизмов и машин" М., "Наука", 1975 г.

2). Дерягин Р.В. "Задания на курсовой проект": Ч.2. – Вологда: ВоПИ, 1983. – 42 с.

3). Дерягин Р.В., Рябинина Л.Н. "Кинематический и силовой анализ плоского рычажного механизма": методические указания к курсовой работе. – Вологда: ВоГТУ, 1999. – 36 с.

4). Попов С.А. "Курсовое проектирование по теория механизмов и механике машин": Учебное пособие для машиностроит. спец. вузов/ Под ред. К.В. Фролова. – М.: Высш. шк., 1986. – 295 с.: ил.

5). "Теория механизмов и машин": Учеб. для втузов/ К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова. – М.: Высш. шк., 1987. – 496 с.: ил.