Реферат: Тригонометричні ефемериди планет Сонячної системи
Це головна формула, яка визначає рух планети по еліптичній орбіті.
Невідоми-
ми величинами тут є AG і AR: геліоцентрична довгота і
радіус-вектор – основ-
ні ефемериди планети з яких в подальшому будуть визначатися інші.
Отже перед початком роботи програми нам відомі елементи орбіти, що є
конс-
тантами, номер дати спостереження , початкові координати планети: геліоцентри-
чна довгота і радіус-вектор в початковий момент часу 9 січня 1990р. Використає-
мо 2 закон Кеплера для опису руху планети. Він говорить, що площа секторів
еліпса орбіти за одинаків проміжок часу однакова. Оскільки швидкість руху
планети по орбіті незмінна, то дуги цих секторів будуть також однакові .
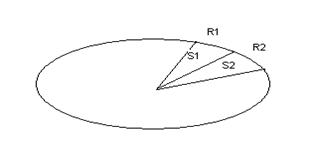S1 = S2 ; R1 = R2
Знаючи елементи орбіти можемо визначити площу всього еліпса орбіти і
поділивши на період обертання визначити площу еліпса за один день (n=1), або
за одну годину чи одну хвилину ( відповідно n=1/24, n=1/1440).
(
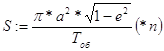в а.о.2 ) ( 3 )
Знаючи орбітальну швидкість (км/с) можемо визначити лінійну довжину дуги
еліпса орбіти за один день ( відповідно за 1 год., за 1 хв. )
R:= vорб * 86400 / AO ( * n ) ( в а.о. ) ( 4 )
де:
86400 – кількість секунд у дні ( 60*60*24 )
AO – астрономічна одиниця
(середня відстань від Землі до Сонця)
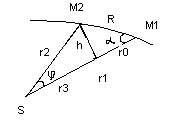
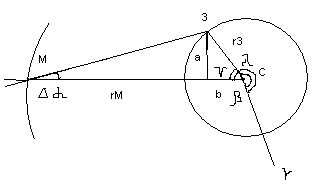
Нам необхідно знайти j - кут переміщення планети за
n-днів.
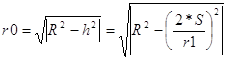
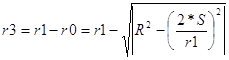
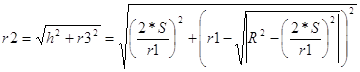( 5 )
(
6 )
Знайдемо довготу
на 10 січня 1990р. : b = bпоч + j . За формулою ( 2 ) визначимо
точніше r2 радіус-вектор на 10 січня 1990р.
На початку циклу обчислень ми посуваємо початковий момент на 1 день ( або
n-днів). В кінці циклу ми прирівнюємо r1:=r2 і перевіряємо чи початковий мо-
мент часу став рівним моменту спостереження.
Другим кроком програми буде знаходження видимих екваторіальних координат планети: пряме піднесення a і схилення d. Пряме піднесення a - вимірюється від точки весняного рівнодення вздовж небесного екватора назустріч видимому добовому обертанню небесної сфери до кола схилень світила і вимірюється в годинній мірі від 0 до 24h ( AA ). Схилення d - вимірюється в градусах від небесного екватора вздовж кола схилень до світила (від–900 до+900 ) ( AB ). Здавалось пряме піднесення a легко визначити розділивши довготу AG на 15 ( 150 = 1 год. ). Однак це було б правильно, якби Земля і планета рухалися на одній прямій від Сонця. Насправді нам необхідно розрахувати зміщення Da скорегувавши таким чином значення AG/15.
(
7 )
тоді AA:=a + Da/15
Схилення планет однозначно визначити не можна . Оскільки площина орбіти
планети нахилена до площини екліптики під кутом і ( Aei ) , то знаючи піднесення
АА визначимо, яке б було схилення планети якби вона рухалася по екліптиці, а
потім скорегуємо його відповідно до нахилу і на Dd.
Схилення d точки екліптики, знаючи його
піднесення a, можна визначити за формулою:
де e - кут
нахилу екліптики до небесного екватора ( 23,50 ).
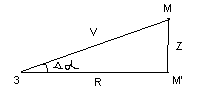
Зміщення Dd можна знайти розв’язавши задачу стереометрії. Виведення
кінце-
вої формули досить велике, тому дамо остаточний результат:
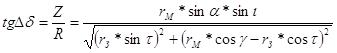( 8 )
де: a = b - W
t = l - b
g = arcsin
( sina * sini )
тоді: AB= d + Dd
Знаючи Z і R з формули ( 8 ) можемо визначити
лінійну відстань між Землею
і планетою
( 9 )
Знаючи AV і екваторіальний радіус планети
можемо визначити видимий кутовий
діаметр планети.
(
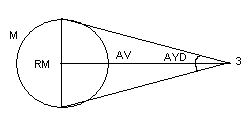
10 )
Фазу планети
визначають так:
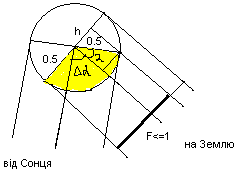
Фаза планети – це її форма, що її
бачить спостерігач із Землі. Вона зумовлена
змінами в умовах освітленості планети Сонцем під час руху навколо нього. В ас-
трономії фазу описують числом – це відношення найбільшої ширини освітленої
частини диска планети до його діаметра.
Важливими ефемеридами планети є умови її видимості, тобто час сходу і заходу азимути точок сходу і заходу на горизонті.
Сходом і заходом світила – називають момент перетину світилом
математичного горизонту, коли воно переходить з невидимої півкулі в видиму і
навпаки. Годинний кут t сходу і заходу світила з координатами a і d на географічній широті j визначають з виразу:
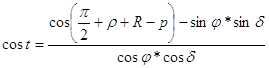(12)
де:
r -
рефракція на горизонті (0,590),
R – кутовий радіус світила (AYD/2),
p – горизонтальний паралакс (RЗ/(AV*AO))
Азимут А світила при сході і заході можна знайти з виразу:
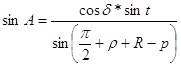(13)
Отже, нам потрібно знайти годинний кут. Годинний кут – це час, що минув з мо-
менту верхньої кульмінації. Годинний кут t визначають за місцевим зоряним ча-
сом спостерігача s і прямим
піднесенням a: t=s-a. Звідси час верхньої
кульмінації
можна знайти за умовою s=a.
оскільки: s = s0 + T0 + 0.0027*T0;
то: a = s0 + T0 * (1.0027);
T0 * (1.0027) = a - s0;
T0 = a - s0 / 1.0027 (14)
де:
s0 – місцевий зоряний час в 0h по всесвітньому часу,
T0 – час кульмінації.
Знаючи час кульмінації, додавши і
віднявши від нього годинний кут сходу і
заходу отримуємо відповідно час сходу і заходу, а далі за формулою (13) азимути
точок сходу і заходу.
Програма містить алгоритми,
які враховують особливості додавання і віднімання годинних величин, адже:
23h + 2h ¹ 25h
23h + 2h = 1h ( 25h – 24h )
2h - 3h ¹ -1h
2h - 3h =23h ( -1h + 24h )
Оскільки початкові координати планет взяті в 0h за всесвітнім часом то
кінцеві
результати також будуть відповідати йому. Щоб привести результати часових
вимірів до місцевого часу спостерігача треба врахувати географічну довготу l
місця спостереження:
Тм = Т0 - l/15 + n
Літній час зумовлює додавання ще однієї години ( n=1 літо, n=0 зима).
2. Розробка алгоритму та структури програми.
Нижчеописана програма на мові Delphi є лише інструментом приблизного
обчислення руху планет Сонячної системи. Програма розбита на кілька структурниx
частин : Form1 ’Ефемериди планет Сонячної
системи’, Form2 ‘Обчислення ефемерид планет
Сонячної системи’, Form3
‘Огляд зоряного неба’, Form4 ‘Детальний огляд зоряного неба’.
У Form1 відображена загальна інформація про курсову роботу. В полі Edit1 ми вводимо пароль і нажимаємо кнопку “Старт”(Button1) для запуску програми. У програмі процедура TForm1.Button1Click порівнює правильність паролю. Якщо пароль вірний сворюється Form2, в протилежному випадку видається повідомлення про невірний пароль. Кнопка “Фініш”( Button2) закриває програму.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8
