Реферат: Спектральный анализ и его приложения к обработке сигналов в реальном времени

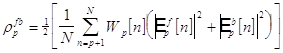
что приводит к следующей оценке :

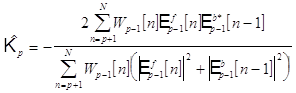
1.4.4. Оценивание линейного предсказания по методу наименьших квадратов.

Налагая ограничения на авторегрессионные параметры, с тем чтобы они удовлетворяли рекурсивному выражению метода Левинсона, в методе Берга происходит минимизация по одного параметра - коэффициента отражения . Более общий подход состоит в минимизации одновременно по всем коэффициентам линейного предсказания.

Итак, пусть для оценивания авторегрессионных параметров порядка p используются последовательность данных .Оценка линейного предсказания вперед порядка p для отсчета будет иметь форму:

где  - коэффициенты линейного предсказания вперед порядка p.

Ошибка линейного предсказания :

В матричном виде это выражение записывается как :

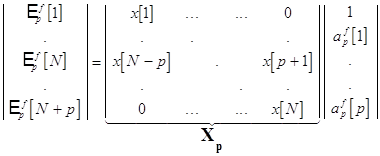
и соотношение для ошибки :

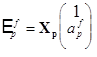
Однако если рассматривать, в котором  минимизируется следующая, невзвешенная  выборочная дисперсия :

то матрица принимает теплицевый вид (далее ее будем обозначать ).

Нормальные уравнения, минимизирующие средний квадрат ошибки имеют следующий вид:

 

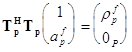
Элементы эрмитовой матрицы имеют вид корреляционных форм

, где

Таким образом, авторегрессионные параметры могут быть получены в результате решения нормальных уравнений. Рассмотрим алгоритм, который в решении нормальных уравнений учитывает тот факт, что эрмитова матрица  получена как произведение двух теплицевых  и в результате этого сводит количество вычислений к  . При использовании алгоритма Холецкого потребовалось бы операций.

Ошибки линейного предсказания вперед и назад p-ого порядка

Здесь вектор данных , вектор коэффициентов линейного предсказания вперед  и вектор линейного предсказания назад определяется следующими выражениями:

 , ,

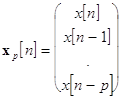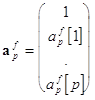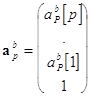
На основе отсчетов измеренных комплексных данных ковариационный метод линейного предсказания позволяет раздельно  минимизировать суммы квадратов ошибок линейного предсказания вперед и назад:

, 

что приводит к следующим нормальным уравнениям :

,

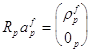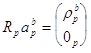
Введем необходимые для дальнейшего определения :

, 

исходя из вида  и  можно записать :

, ,

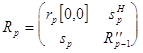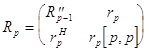где вектор столбцы  и даются выражениями :

,

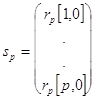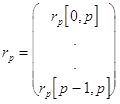
Важными также являются следующие выражения :

Пара векторов-столбцов и  определяются из выражений :

Аналогично определяются вектора и , а также и  через матрицы  и .

Процедура, используемая для обновления порядка вектора линейного предсказания вперед выглядит следующим образом :

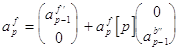, где 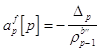, в котором

Соответствующий вид имеет процедура обновления порядка для вектора предсказания назад:

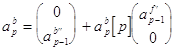, где ,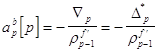

Векторы и должны удовлетворять следующим рекурсиям обновления порядка:

Используя тот факт, что  является эрмитовой матрицей имеем следующие выражения для  и :

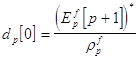
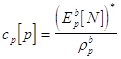
Введем скалярные множители

 

Соответствующие рекуррентные выражения для  и имеют следующий вид :

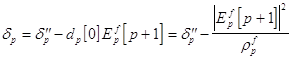
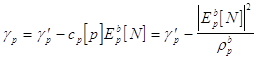
Наконец, еще одна рекурсия обновления порядка необходима для вектора  :

 

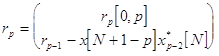
Обновление временного индекса в векторе коэффициентов линейного предсказания вперед осуществляется в соответствии с выражением :

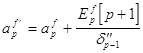
Выражение для обновления временного индекса у квадрата ошибки линейного предсказания вперед :

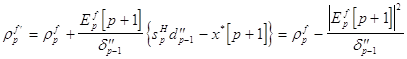
Аналогичным образом обновление временного индекса в векторе коэффициентов линейного предсказания назад ведется в соответствии с выражением :

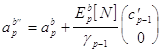
Выражение для обновления временного индекса у квадрата ошибки линейного предсказания назад :

, 

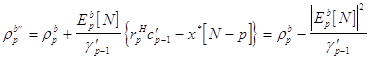
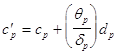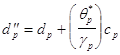
где комплексный скаляр удовлетворяет выражениям :

Соответствующие рекурсии по временному индексу для действительных скаляров  и  даются следующими выражениями:

Страницы: 1, 2, 3, 4, 5, 6, 7, 8