Реферат: Спектральный анализ и его приложения к обработке сигналов в реальном времени

Эффект неявно присутствующего окна из-за конечности данных приводит к свертке истинной спектральной плотности с преобразованием Фурье дискретно-временного прямоугольного или треугольного (как в случае со смещенными оценками) окна. Для уменьшения этого эффекта используется корреляционное окно и коррелограммная оценка спектральной плотности мощности в общем виде выглядит следующим образом:

Экспериментальные результаты приведены в соответствующем разделе.

1.3.5. Область применения.

Классические методы спектрального анализа применимы почти ко всем классам сигналов и шумов в предположении о стационарности. Вычислительная эффективность периодограммных и коррелограммных методов основана на использовании алгоритма Быстрого Преобразования Фурье. Недостатком всех методов спектрального анализа является искажения в спектральных составляющих по боковым лепесткам из-за взвешивания данных при помощи окна. Сравнение экспериментальных результатов с другими методами и характеристики взвешивающих окон приведены в соответствующем разделе.

1.4. Авторегрессионное спектральное оценивание.

1.4.1. Введение

Одна из причин применения параметрических моделей случайных и процессов и построения на их основе методов получения оценок спектральной плотности мощности обусловлена увеличением точности оценок по сравнению с классическими методами. Еще одна важная причина  - более высокое спектральное разрешение. Далее рассматриваются следующие методы: метод Юла-Уалкера оценивания авторегрессионных параметров по последовательности оценок автокорреляционной функции, метод Берга оценивания авторегрессионных параметров по последовательности оценок коэффициентов отражения, метод раздельной минимизации квадратичных ошибок линейного предсказания вперед и назад - ковариационный метод, метод совместной минимизации квадратичных ошибок прямого и обратного линейного предсказания - модифицированный ковариационный.  

Модель временного ряда (называемая модели авторегрессии-скользящего среднего в случае входной последовательности - белого шума), которая пригодна для аппроксимации многих встречающихся на практике детерминированных и стохастических процессов с дискретным временем, описывается следующим разностным уравнением:

Системная функция , связывающая вход и выход этого фильтра имеет рациональную форму:

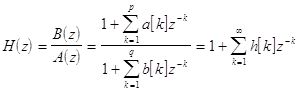
Если в качестве входной последовательности использовать белый шум, то приходим к АРСС-модели. Спектральную плотность для АРСС-модели получаем, подставляя , что дает

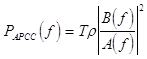, где

, , а  - дисперсия

возбуждающего белого шума

В частных случаях для авторегрессионной модели и модели скользящего среднего получаем соответственно :

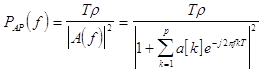
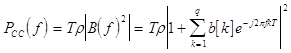
1.4.2. Оценивание корреляционной функции - метод Юла-Уалкера.

Из соотношения, связывающего параметры АРСС-модели с порядком авторегрессии p и скользящего среднего q:

Поскольку полагается, что u[k] - белый шум, то  

,

, m>q

, m<0

В частном случае для авторегрессионных параметров, получаем :

,

, m=0

, m<0

В матричном виде эти соотношения выглядят следующим образом :

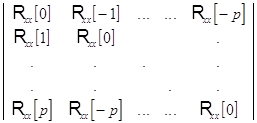
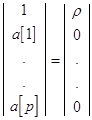
Таким образом, если задана автокорреляционная последовательность для , то АР-параметры можно найти в результате решения последнего матричного соотношения (называемого нормальными уравнениями Юла-Уалкера), где автокорреляционная матрица является и теплицевой, и эрмитовой.

Наиболее очевидным подходом к авторегрессионному оцениванию является решение нормальных уравнений Юла-Уалкера, в которые вместо значений неизвестной автокорреляционной функции подставляем их оценки. Результаты экспериментов с этим, первым методом АР-оценивания и сравнение с другими методами этого класса приведены в соответствующем разделе.

1.4.3. Методы оценивания коэффициентов отражения.

Рекурсивное решение уравнений Юла-Уалкера методом Левинсона связывает АР-параметры порядка p c параметрами порядка p-1 выражением :

, где n=1,2,..p-1

Коэффициент отражения определяется по известным значениям автокорреляционной функции :

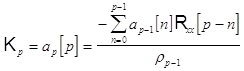
, где

Из всех величин только  непосредственно зависит от автокорреляционной функции. В разное время предлагалось несколько различных процедур оценки коэффициента отражения, рассмотрим некоторые из них.

1.4.3.1. Геометрический алгоритм.

Ошибки линейного предсказания вперед и назад определяются соответственно следующими выражениями:

 

Рекурсивные выражения, связывающие ошибки линейного предсказания моделей порядков p и p-1, определяются простой подстановкой   и в рекурсивное соотношение для авторегрессионных параметров:

Несложно показать, что коэффициент отражения обладает следующим свойством (является коэффициентом частной корреляции между ошибками линейного предсказания вперед и назад) :

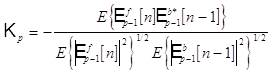
Используя оценки взаимной корреляции и автокорреляции ошибок предсказания вперед и назад, получим :

 

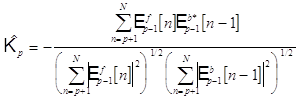
Таким образом, геометрический алгоритм использует алгоритм Левинсона, в котором вместо обычного коэффициента отражения, вычисляемого по известной автокорреляционной функции, используется его оценка 

Окончательный вид выражений геометрического алгоритма :

, где n=1,2,..p-1

,  

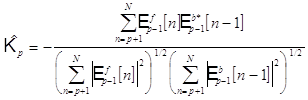
, где

1.4.3.2. Гармонический алгоритм Берга.

Алгоритм Берга идентичен геометрическому, однако оценка коэффициента отражения находится из других соображений, а именно : при каждом значений параметра p в нем минимизируется арифметическое среднее мощности ошибок линейного предсказания вперед и назад (то есть выборочная дисперсия ошибки предсказания):

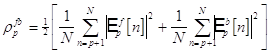
Приравнивая производные к нулю, имеем оценку для  :

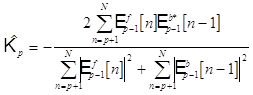
Некоторым обобщением является взвешивание среднего квадрата ошибки предсказания для уменьшения частотного смещения, наблюдаемого при использовании базового метода Берга:

Страницы: 1, 2, 3, 4, 5, 6, 7, 8