Быстрый поиск

Реферат: СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ В ЛИНЕЙНОЙ ЗАДАЧЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ

Этот процесс часто называют процессом преследования. Так как , то , и Mi+1 – трехдиагональная матрица, точно так же, как и Mi. Начальный угол можно выбрать так, чтобы преобразование было QR–преобразованием со сдвигом, равным s.

Обычный QR–алгоритм со сдвигом можно записать в следующем виде:

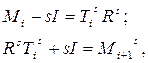
где – верхняя треугольная матрица. Следовательно, . Параметр сдвига s определяется собственным значением нижнего минора (размерности 2´2) матрицы Mi. При таком выборе параметра s метод обладает глобальной и почти всегда кубичной сходимостью.

2.3. Пример сингулярного разложения

Проведем преобразование Хаусхолдера на матрице ,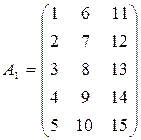

К первой компоненте первого столбца прибавляем норму первого столбца, получим 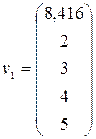. Пусть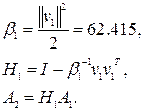

Преобразованная матрица A2 вычисляется следующим образом. Для первого столбца имеем:

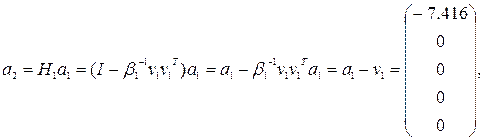
так как

Таким образом, в первый столбец были введены нули и его длина не изменилась. Получим второй столбец:

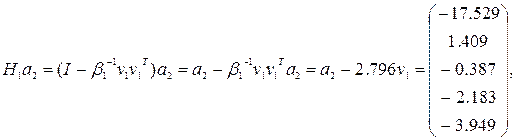
для третьего столбца:

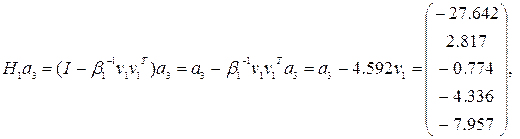
окончательно,

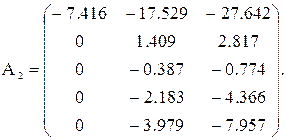
Столбцы матрицы A2 получаются вычитанием кратных вектора v1 из столбцов A1. Эти кратные порождаются скалярными произведениями, а не отдельными элементами, как в гауссовом исключении.

Прежде чем вводить дальнейшие нули под диагональю, преобразованием вида A3=A2Q1, получают нули в первой строке. Нули уже стоящие в первом столбце, не должны быть испорчены, длина первого столбца должна быть сохранена; поэтому при внесении нулей в первую строку нельзя менять первый элемент строки, изменяем второй элемент и зануляем третий. Для матрицы большего размера на этом шаге было бы получено n–2 нуля.

Преобразование порождается первой строкой A2:

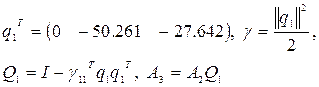
Строка матрицы A3 с номером i получается по формуле

Таким образом, из каждой строки A2 вычитается надлежащее кратное . Это дает матрицу

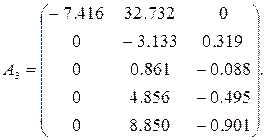
Поскольку первая компонента нулевая, то нули первого столбца A2 сохраняются в A3, Так как Q1 ортогональная, то длина каждой строки в A3 равна длине соответствующей строки в A2.

Теперь можно добиться новых нулей под диагональю, не испортив полученных ранее:

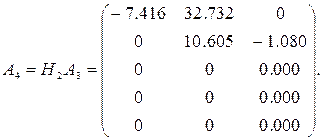
Поскольку ранг этой матрицы равен лишь 2, то теперь третий столбец имеет на диагонали и под диагональю элементы порядка ошибки округления. Эти элементы обозначены в матрице через 0.000, чтобы отличить их от элементов, в точности равных нулю. Если бы матрица имела полный ранг, то нужно было бы выполнить еще одно преобразование, чтобы получить нули в третьем столбце:

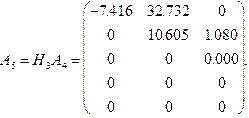
Если бы не ошибки округлений, то в данном примере третий диагональный элемент был бы точным нулем. Элементы под диагональю во всех столбцах указаны как точные нули, потому что преобразования так и строились, чтобы получить там нули. Последнее преобразование H3 в этом примере могло бы быть тождественным, однако тогда оно не было бы хаусхолдеровым отражением. Фактически использование H3 попутно изменяет знак элемента – 1.080 в матрице A4.

Получилась искомая двухдиагональная матрица, и первый этап закончен. Прямое использование ортогональных преобразований не позволяет получить какие–либо новые нули. Для общего порядка n нужно n преобразований H и n–2 преобразований Q, чтобы достигнуть данного места. Число преобразований не зависит от строчной размерности m, но от m зависит работа, затрачиваемая на выполнение каждого преобразования.

глава 3. Использование сингулярного разложения в методе наименьших квадратов

При использовании метода сингулярного разложения (SVD – Singular Value Decomposition) мы проводим разложение для матрицы плана. При этом основное уравнение y=Xb приобретает вид y=USVTb. Отсюда следует, что коэффициенты b можно получить решая уравнение UTy=SVTb. Т.е. если все sj, j=1,…,n, являющиеся диагональными элементами S отличны от нуля, то последнее уравнение разрешимо и

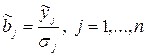, где .

Однако такое решение не всегда желательно, если некоторые sj малы. Для правильного использования метода SVD мы должны ввести границу t отражающую точность входных данных и точность использованной плавающей арифметики. Всякое sj, большее, чем t, приемлемо, и соответствующее вычисляется по (1.20). Любое sj, меньшее, чем t, рассматривается как пренебрежимо малое, и соответствующему может быть придано произвольное значение. С этой произвольностью значений связана не единственность набора коэффициентов, получаемых методом наименьших квадратов. Изменения входных данных и ошибки округлений, меньшие, чем t, могут привести к совершенно другому набору коэффициентов, определяемых этим методом. Поскольку обычно желательно, чтобы эти коэффициенты были по возможности малы, то полагаем =0, если sj £t.

Отбрасывание чисел sj, меньших, чем t, приводит к уменьшению числа обусловленности с до . Поскольку число обусловленности является множителем в увеличении ошибки, то следствием будет более надежное определение коэффициентов .

Продемонстрируем использование метода на следующем примере:

t	Y
1900	75994575
1910	91972266
1920	105710620
1930	123203000
1940	131669275
1950	150697361
1960	179323175
1970	203211926

Следует определить значение Y при X =1980.

Если аппроксимировать эти данные квадратичным многочленом и использовать двойную точность, то в результате получим следующие коэффициенты . При одинарной точности вычислений коэффициенты будут иметь значения . У этих двух наборов коэффициентов не совпадают даже знаки. Если такую модель использовать для предсказания, то для коэффициентов, вычисленных с двойной точностью, прогноз будет Y=227780000 , а для обычной точности Y=145210000. Ясно, что второй набор коэффициентов бесполезен. Исследуем достоверность результатов. Матрица плана для данного примера имеет размеры 8 ´ 3

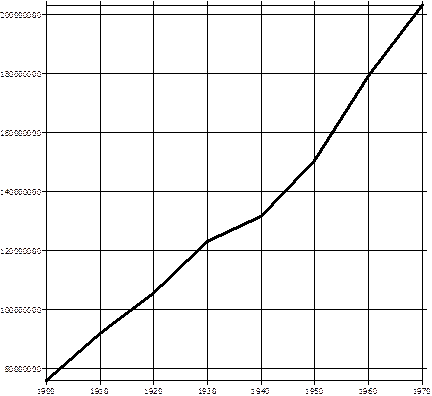
Рис. 2. Численный пример

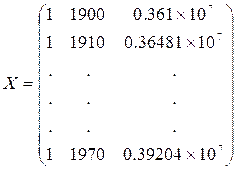
Ее сингулярные числа: .

Число обусловленности равно , что говорит о близости базисных функций 1, t и t2 к линейной зависимости. Для того, чтобы исправить ситуацию можно предпринять одну из следующих мер.