Быстрый поиск

Реферат: СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ В ЛИНЕЙНОЙ ЗАДАЧЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ

. (13)

Исследование матрицы X'X в факторном анализе называется R-модификацией, а XX' – Q–модификацией. Соотношения (12)–(13) показывают, что результаты Q–модификации можно получить по результатам R–модификации и наоборот.

Практическая последовательность нахождения сингулярного разложения следующая.

1. Вычисляется X'X или XX', в зависимости от того, порядок какой матрицы меньше. Предположим, что в данном случае это X'X.

2. Вычисляются положительные собственные числа матрицы X'X и соответствующие им собственные векторы .

3. Находятся сингулярные числа .

4. Вычисляются по соотношению (11).

Пусть в разложении (11) собственные числа расположены в порядке убывания. Аппроксимационные свойства соотношения (11) являются еще более фундаментальными, чем само соотношение. Эти свойства вытекают из решения следующих двух задач.

Задача 1. Дана симметричная матрица S, порядка pxp и ранга r с неотрицательными собственными значениями. Требуется найти симметричную матрицу Т, размерности pxp, с неотрицательными собственным значениями заданного ранга k, k<r, являющуюся наилучшей аппроксимацией матрицы S в смысле наименьших квадратов.

Задача 2. Дана прямоугольная матрица X, порядка Nxp и ранга r и число k<r. требуется найти матрицу W порядка pxp и ранга k, наилучшим образом аппроксимирующую матрицу X в смысле наименьших квадратов.

Решением этих двух задач являются матрицы:

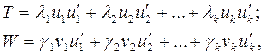(14)

представляющие собой суммы k первых членов в соответствующем разложении. Матрицы T и W называются наилучшими в смысле наименьших квадратов “матричными аппроксимациями меньшего ранга” для матриц S и X соответственно. Свойство наилучшей аппроксимации в смысле наименьших квадратов можно выразить следующим образом: матрица T ближе всего к матрице S в том смысле, что сумма квадратов всех элементов матрицы S–T минимальна. Аналогично матрица W ближе всего к матрице X в том смысле, что минимальна сумма квадратов элементов матрицы X–W. Мерой близости или качества аппроксимации считается относительная величина , т.е. сумма r–k наименьших собственных чисел матрицы X’X. Иногда мерой качества аппроксимации считается относительная величина

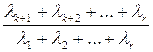(15)

или функция от нее.

Рассмотрим наиболее распространенный случай p=r.

Матрица S может быть ковариационной матрицей p линейно независимых переменных. Матрица T также может представлять собой ковариационную матрицу p переменных, но так как ранг матрицы T k<p, то эти p переменных линейно зависят от k переменных. Таким образом, p исходных переменных, ковариационная матрица которых есть S, могут быть приближенно выражены через k переменных.

Во второй задаче исходную матрицу X порядка Nxp можно выразить как X=VГU’, где V – матрица порядка Nxp c ортонормированными столбцами; Г – диагональная матрица порядка pxp, а U – квадратная ортогональная матрица порядка pxp.

Матричную аппроксимацию меньшего ранга W можно представить в виде

где – состоит из первых k столбцов матрицы V, – из первых k строк или столбцов матрицы Г, а – из первых k столбцов матрицы U. поскольку W»X, то

(16)

При умножении этой матрицы справа на получаем

(17)

Матрица порядка pxk определяет преобразование строк матрицы X из евклидова p–мерного пространства в евклидово k–мерное пространство; уравнение (16) показывает, что существует преобразование матрицы X порядка Nxp в матрицу порядка Nxk. Матрица X содержит N точек в p–мерном евклидовом пространстве, которые приближенно могут быть спроектированы в k–мерное евклидово пространство. матрица определяет координаты этих точек в k–мерном евклидовом пространстве.

1.5. QR–разложение

Теорема 2. Пусть А – m´n–матрица. Существует ортогональная m´m–матрица Q такая, что в матрице QA=R под главной диагональю стоят только нулевые элементы.

Доказательство. Выберем ортогональную m´m–матрицу Q в соответствии с преобразованием Хаусхолдера (9), так, чтобы первый столбец Q1A имел нулевые компоненты со 2–ой по m–ю. Далее выбираем ортогональную (m-1)´(m–1)–матрицу P2 следующим образом. Будучи применена к m–1 вектору, составленному из компонент со 2–ой по m–ю второго столбца матрицы Q1A, она аннулирует компоненты с 3–ей по m–ю этого вектора. Матрица преобразования

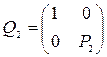
ортогональна, и Q2Q1A имеет в первых двух столбцах нули под главной диагональю. Продолжая таким образом, можно построить произведение, состоящее максимум из n ортогональных преобразований, которое трансформирует А к верхней треугольной форме. Формальное доказательство можно получить методом конечной индукции.

Полученное представление матрицы произведением ортогональной и верхней треугольной матриц называется QR–разложением.

Теорема 3. Пусть А – m´n–матрица ранга к, причем k<n£m. Существуют ортогональная m´m–матрица Q и m´n–матрица перестановки P такие, что

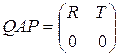, (18)

где R – верхняя треугольная к´к–матрица ранга к.

Доказательство. Выберем матрицу перестановки Р таким образом, чтобы первые к столбцов матрицы AP, были линейно независимы. Согласно теореме 2, найдется ортогональная m´m–матрица Q такая, что QAP будет верхней треугольной. Поскольку первые к столбцов АР линейно независимы, это будет верно для первых к столбцов QAP.

Все элементы матрицы QAP, стоящие на пересечении строк с номерами к+1,...,m и столбцов с номерами к+1,...,n, будут нулями. В противном случае rankQAP>k, что противоречит предположению rankA=k. Итак, QAP имеет форму, указанную правой частью (4). Теорема доказана.

Подматрицу [R:T] из правой части (18) можно теперь преобразовать к компактной форме, требуемой от матрицы R из теоремы 2. Это преобразование описывает следующая лемма.

Лемма 1. Пусть [R:T] – к´к–матрица, причем R имеет ранг к. Существует ортогональная n´n–матрица W такая, что

где – нижняя треугольная матрица ранга к.

Доказательство леммы вытекает из теоремы 3, если отождествить величины n, k, [R:T], W из формулировки леммы с соответствующими величинами m, n, AT, QT теоремы 3.

Используя теорему 3 и лемму 1 можно доказать следующую теорему.

Теорема 4. Пусть А – m´n–матрица ранга к . Найдутся ортогональная m´m–матрица Н и ортогональная n´n–матрица К такие, что

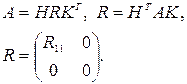(19)