Быстрый поиск

Реферат: Разработка схемы электронного эквалайзера

3) найти коэффициенты фильтра, взяв дискретные значения импульсной переходной функции k(nT).

Определение порядка и синтез коэффициентов

Цифровых фильтров, входящих в состав эквалайзера.

Предположим, что ФЧХ равна 0. Тогда для получения импульсной переходной функции полосового фильтра с полосой пропускания fi-1 ÷ fi достаточно взять обратное преобразование Фурье от АЧХ:

k(t) = 1/2π∫A(ω) ٠ejωtdω = A0/2π∫ejωtdω - A0/2π∫ejωtdω =

=A0/πt(sinωi٠t - sinωi-1٠t), где ωi = 2π fi.

Для исключения погрешности дискретизации выберем частоту дискретизации в два раза выше верхней частоты общей полосы пропускания эквалайзера:

Tд = 2π/ωд = 2π/2ωn = π/ωn = π/(2٠π٠13) = 0,0385 мс.

Продискретизировав импульсную переходную функцию с периодом дискретизации, получим решетчатую функцию k(nTд).

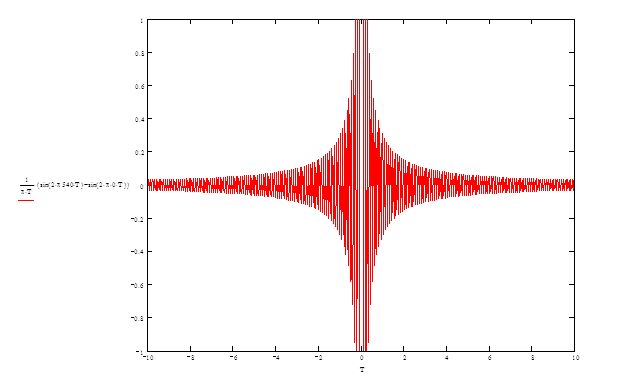
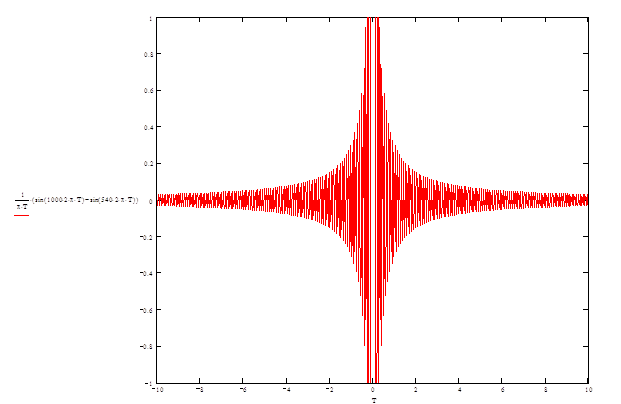
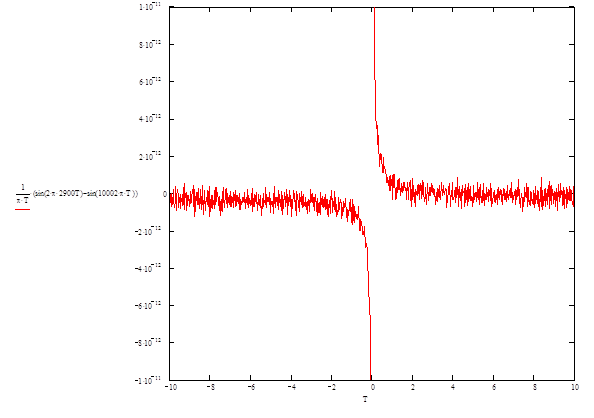
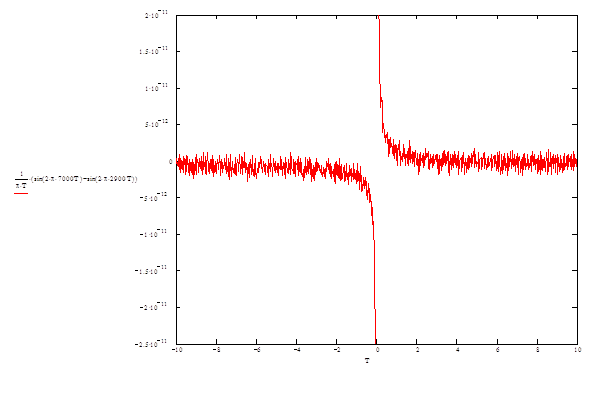
Импульсная переходная функция начинается слева от начала координат. Это невозможно с физической точки зрения, так как нельзя реагировать на событие, которое еще не произошло. Чтобы сместить функцию по оси абсцисс вправо, необходимо внести запаздывание. Однако, если импульсная переходная функция бесконечна, то необходимо внести бесконечное запаздывание, что невозможно. Реально берут 2N+1 отсчетов решетчатой функции, что соответствует запаздыванию на NTд.

В рамках курсового проекта порядок фильтра ограничивается следующей величиной:

N ≥ tдоп/Tд,

где tдоп – время, через которое k(t) ≤ 0,1٠k0,

k0 = k(t)max.

Фильтр нижних частот (ФНЧ).

Частота среза фильтра: кГц;

рад/с;

Частота дискретизации кГц;

Период дискретизации фильтра для определения порядка данного фильтра:

мс.

Переходная функция :

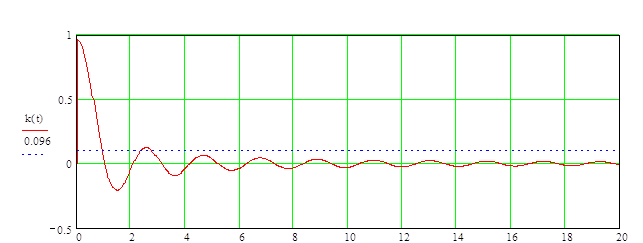
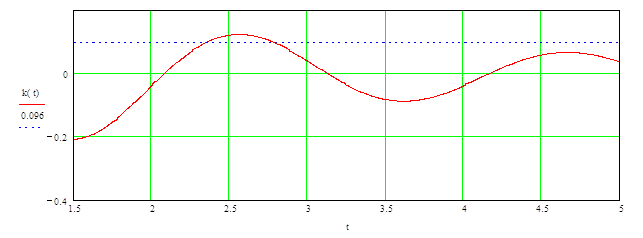Рис.3. Переходная функция ФНЧ.

Определим коэффициенты фильтра ФНЧ:

Таблица 2.

n a n a n a n a

0	-0,050849552	21	0,05213266	41	-0,057902897	61	0,066693601
1	-0,047381452	22	0,044603043	42	-0,046254347	62	0,047455709
2	-0,042531604	23	0,035644122	43	-0,032920949	63	0,02589646
3	-0,036405607	24	0,025465445	44	-0,018209385	64	0,002473637
4	-0,029146011	25	0,014314951	45	-0,00247349	65	-0,022284955
5	-0,020929191	26	0,002473283	46	0,013893446	66	-0,047790903
6	-0,011961243	27	-0,009752894	47	0,030467601	67	-0,073406266
7	-0,002473018	28	-0,02203843	48	0,046804595	68	-0,098456107
8	0,007285626	29	-0,034047894	49	0,062450287	69	-0,122242231
9	0,017052183	30	-0,045444252	50	0,07695216	70	-0,144057845
10	0,026558333	31	-0,055897815	51	0,089871011	71	-0,163202823
11	0,035537068	32	-0,065095206	52	0,100792694	72	-0,178999256
12	0,04372993	33	-0,072748139	53	0,109339601	73	-0,190806934
13	0,050894174	34	-0,078601768	54	0,115181622	74	-0,198038431
14	0,056809654	35	-0,082442378	55	0,118046281	75	-0,200173423
15	0,061285263	36	-0,084104208	56	0,117727803	76	-0,196771935
16	0,06416472	37	-0,083475205	57	0,114094848	77	-0,187486186
17	0,065331569	38	-0,080501546	58	0,107096699	78	-0,172070753
18	0,064713212	39	-0,075190761	59	0,096767723	79	-0,150390796
19	0,062283872	40	-0,067613365	60	0,083229939	80	-0,122428134
20	0,058066372