 Реферат: Разработка системы задач (алгоритмы-программы) по дискретной математике
Реферат: Разработка системы задач (алгоритмы-программы) по дискретной математике
Реферат: Разработка системы задач (алгоритмы-программы) по дискретной математике
Вятский Государственный Гуманитарный Университет
Кафедра прикладной математики
Курсовая работа по информатике
Тема: Разработка системы упражнений и задач (алгоритмы-программы) по дискретной математике.
Выполнил:Студент 4 курса
факультета информатики
Лепешкин Антон Геннадъевич
Проверила: Ашихмина Татьяна Викторовна
Киров
2004
Содержание.
Введение. 3
Глава 1 Теоретический материал. 4
Перебор с возвратом. 4
Поиск данных. 5
Логарифмический(бинарный) поиск. 5
Методы сортировки. 6
Сортировка слияниями. 6
Быстрая сортировка Хоара. 6
Графы. 6
Представление графа в памяти компьютера. 6
Достижимость. 7
Кратчайшие пути. 8
Алгоритм Дейкстры.. 8
Алгоритм Флойда (кратчайшие пути между всеми парами вершин). 9
Глава 2 Система задач и упражнений. 9
Классификация задач. 9
Комнаты музея. 12
Пират в подземелье. 13
Диспетчер и милиция. 14
Задача о футболистах. 15
Задача о семьях. 16
Метро. 16
Роботы. 17
Вожатый в лагере. 20
Егерь. 21
Игра «Найди друга». 22
Приложение. 22
1. 22
2. 25
3. 27
4. 30
5. 32
6. 32
7. 34
8. 39
9. 41
10. 43
Заключение. 45
Литература.. 45
Несмотря на то, что для решения задач в основном используются общие методы, все-таки мышление каждого конкретного человека немного отличается от мышления других людей, если он обладает достаточной базой знаний. Таким образом, при решении задач «начиная с нуля» можно зайти в тупик, если выбрать неверный путь решения задачи. В данном курсовом проекте мы разработаем собственную классификацию задач, позволяющую определить наиболее подходящий способ решения, чтобы облегчить процесс моделирования и составления алгоритма и предотвратить выбор неверного способа, также рассмотрим данную классификацию с точки зрения методики преподавания информатики. выбор неверного способа. В этом заключается актуальность данного курсового проекта.
Цель: Разработать собственную классификацию для задач по дискретной математике. Для достижения этой цели были поставлены следующие задачи:
1) Разработать собственную систему задач и упражнений по дискретной математике.
2) Определить способы решения данных задач, используя теоретический материал курса дискретной математики.
3) Составить алгоритм – программу для каждой задачи, реализующий выбранный способы решения.
4) Разработать систему критериев классификации данной системы задач.
Глава 1
Теоретический материал.
Перебор с возвратом.
Общая схема
Даны N упорядоченных множеств U1 U2,..., Un (N - известно), и требуется построить вектор А=(а1 а2, ..., аn), где a1€U1, a2€U2, ..., an€Un, удовлетворяющий заданному множеству условий и ограничений.
 В алгоритме перебора вектор А строится
покомпонентно слева
В алгоритме перебора вектор А строится
покомпонентно слева
направо. Предположим, что уже найдены значения первых (к-1)
компонент, A=(a1, a2, ..., a(k-1)),
?, ..., ?), тогда заданное множество
условий ограничивает выбор следующей компоненты аk некоторым
множеством SkCUk. Если Sk<>[ ] (пустое), мы вправе
выбрать в
качестве ак
наименьший элемент Sk и
перейти к выбору ^/^ "^выборы п«я»,
(к+1) компоненты и
так далее. Однако /[ ■ Д Jfcv при данном а,
если условия условия
| а,, ^иаз |
таковы, что Sk оказалось пустым, то мы возвращаемся к выбору
(к-1) компоненты, отбрасываем
а(k-1) и выбираем в качестве нового a(k-1) тот элемент S(k-i), который непосредственно следует за только что отброшенным. Может оказаться, что для нового a(k-1) условия задачи допускают непустое Sk, и тогда мы пытаемся снова выбрать элемент ак. Если невозможно выбрать a(k-1), мы возвращаемся еще на шаг назад и выбираем новый элемент а(к-2) и так далее.
Графическое изображение - дерево поиска. Корень дерева (0 уровень) есть пустой вектор. Его сыновья суть множество кандидатов для выбора а1 и, в общем случае, узлы k-го уровня являются кандидатами на выбор ак при условии, что а1, а2, ..., a(k-1) выбраны так, как указывают предки этих узлов. Вопрос о том, имеет ли задача решение, равносилен вопросу, являются ли какие-нибудь узлы дерева решениями. Разыскивая все решения, мы хотим получить все такие узлы.
Рекурсивная схема реализации алгоритма,
procedure Backtrack(Beктop,i);
begin
if <вектор является решением> then <записать его>
else begin <вычислить Si>;
for a€Si do Васкtrаск(вектор| | a,i+l);
end; end;
Оценка временной сложности алгоритма. Данная схема реализации перебора приводит к экспоненциальным алгоритмам. Действительно, Пусть все решения имеют длину N, тогда исследовать требуется порядка | Si| *| S2| *...*| SN| узлов дерева. Если значение S; ограничено некоторой константой С, то получаем порядка CN узлов.
Поиск данных.
Логарифмический(бинарный) поиск
Логарифмический (бинарный или метод деления пополам) поиск данных применим к сортированному множеству элементов а1 < а2 < ... < ап, размещение которого выполнено на смежной памяти. Для большей эффективности поиска элементов надо, чтобы пути доступа к ним стали более короткими, чем просто последовательный перебор. Наиболее очевидный метод: начать поиск со среднего элемента, т.е. выполнить сравнение с элементом а. Результат сравнения позволит определить, в какой половине последовательности а{, а2,..., а, 1+„ ,,..., ап продолжить поиск,
применяя к ней ту же процедуру, и т.д. Основная идея бинарного поиска довольно проста, однако «для многих хороших программистов не одна попытка написать правильную программу закончилась неудачей». Чтобы досконально разобраться в алгоритме, лучше всего представить данные ах < а2 < ... < ап в виде двоичного дерева сравнений, которое отвечает бинарному поиску.
Двоичное дерево называется деревом сравнений , если для любой его вершины (корня дерева или корня поддерева) выполняется условие:
{Вершины левого поддерева}<Вершина корня<{Вершины правого поддерева }.
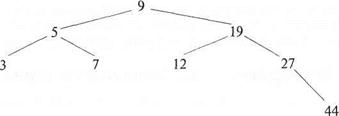
Рис. Пример дерева сравнений, отвечающего бинарному поиску среди сортированных элементов: 3,5,7,9,12,19,27,44
Т.о. бинарный поиск – это сравнение эталона х, которое осуществляется с элементом, расположенным в середине массива и в зависимости от результата сравнения (больше или меньше) дальнейший поиск проводится в левой или правой половине массива.
Используется, когда имеется какая-либо информация о массиве, например массив упорядочен по неубыванию. Общее количество сравнений имеет порядок О(N*logN).
Методы сортировки.
Сортировка слияниями.
Используется, когда необходимо объединить упорядоченные фрагменты массивов: A[k],…,A[m] и B[m+1],…,B[q] в один C[k],…,C[q], тоже упорядоченный (k<=m<=q). Основная идея решения состоит в сравнении очередных элементов каждого фрагмента, выяснении, какой из элементов меньше, переносе его во вспомогательный массив С (для простоты) и продвижении по тому фрагменту массива, из которого взят элемент. При этом следует не забыть записать в С оставшуюся часть того фрагмента, который не успел себя «исчерпать».
Метод слияний – один из первых в теории алгоритмов сортировки. Он предложен Дж. Фон Нейманом в 1945 году. Эффективность алгоритма, по Д. Кнуту, составляет С=О(N*logN).
Быстрая сортировка Хоара.
Метод предложен Ч.Э.Р.Хоаром в 1962 году.
Идея метода. В исходном массиве А выбирается некоторый элемент Х (барьерный элемент). Основной целью алгоритма является запись Х «на свое место» в массиве, пусть это будет место k, такое, что слева от Х были элементы массива, меньшие или равные Х, а справа – элементы массива, большие Х, т.е. массив А будет иметь вид: (А[1],A[2],…,A[k-1]),A[k] (X), (A[k+1],…, A[n]).
В результате элемент A[k] находится на своем месте и исходный массив А разделен на две неупорядоченные части, барьером между которыми является элемент A[k]. Дальнейшие действия очевидны – независимо сортировать полученные части по той же логике до тех пор, пока не останутся части массива, состоящие из одного элемента, то есть пока не будет отсортирован весь массив.


