 Реферат: Разработка и исследование имитационной модели разветвленной СМО (системы массового обслуживания) в среде VB5
Реферат: Разработка и исследование имитационной модели разветвленной СМО (системы массового обслуживания) в среде VB5
СМО с очередью подразделяются на разные виды, в зависимости от того, как организована очередь — ограничена она или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания (так называемые «СМО с нетерпеливыми заявками»). При анализе СМО должна учитываться также и «дисциплина обслуживания» — заявки могут обслуживаться либо в порядке поступления (раньше пришла, раньше обслуживается), либо в случайном порядке. Нередко встречается так называемое обслуживание с приоритетом — некоторые заявки обслуживаются вне очереди. Приоритет может быть как абсолютным — когда заявка с более высоким приоритетом «вытесняет» из-под обслуживания заявку с низшим, так и относительным — когда начатое обслуживание доводится до конца, а заявка с более высоким приоритетом имеет лишь право на лучшее место в очереди.
Существуют СМО с так называемым многофазовым обслуживанием, состоящим из нескольких последовательных этапов или «фаз» (например, покупатель, пришедший в магазин, должен сначала выбрать товар, затем оплатить его в кассе, после чего получить на контроле).
Кроме этих признаков, СМО делятся на два класса: «открытые» и «замкнутые». В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии находится сама СМО (сколько каналов занято). В замкнутой СМО — зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже неисправно и ждет наладки. Это — пример замкнутой СМО.
Рассмотрим вывод упомянутой ранее формулы Литтла, связывающей (для предельного, стационарного режима) среднее число заявок Lсист, находящихся в системе массового обслуживания (т. е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе Wсист.
Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или с ограниченной очередью) и связанные с нею два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее, так как оба потока имеют одну в ту же интенсивность l.
Обозначим: X(t)—число заявок, прибывших в СМО до момента t, Y(t) — число заявок, покинувших СМО до момента t. И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок (X(t)) и уходов заявок (Y(t)). Для любого момента t их разность Z(t) = X(t) - Y(t) — это число заявок, находящихся в СМО.
Рассмотрим очень большой промежуток времени T и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z(t) на этом промежутке, деленному на длину интервала T:
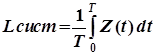 (7)
(7)
Данный интеграл представляет собой площадь фигуры, заключенной между X(t) и Y(t). Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т. д.). Обозначим эти времена как t1, t2,... Правда, под конец промежутка Т некоторые прямоугольники войдут в эту фигуру не полностью, а частично, но при достаточно большом Т этим можно пренебречь. Таким образом, можно считать, что
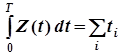 , (8)
, (8)
где сумма распространяется на все заявки, пришедшие за время Т.
Разделим правую и левую часть (8) на длину интервала Т. Получим, с учетом (7):
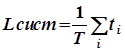 (9)
(9)
Разделим и умножим правую часть (9) на интенсивность l:
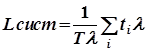 (10)
(10)
Величина Tl — это среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен ti на среднее число заявок, то получим среднее время пребывания заявки в системе Wсист- Итак,
![]() (11)
(11)
Это и есть формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.
Точно таким же образом выводится вторая формула Литтла, связывающая среднее время пребывания заявки в очереди Wоч и среднее число заявок в очереди Lоч.
Lоч = l Wоч
2.3 Варианты систем массового обслуживания
1. n-канальная СМО с отказами
A — абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени);
Q — относительная пропускная способность (средняя доля пришедших заявок, обслуживаемых системой);
Pотк — вероятность того, что заявка покинет СМО необслуженной;
![]() — среднее число занятых каналов;
— среднее число занятых каналов; ![]() ;
;
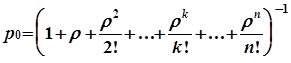 ;
; 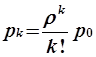 ;
;
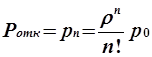 ;
; 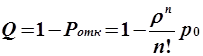 ;
;
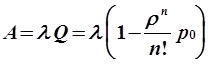 ;
; 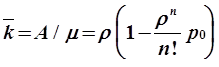
2. Одноканальная СМО с неограниченной очередью
Pзан — вероятность того, что канал занят; Lоб — среднее число заявок под обслуживанием
![]() ;
; ![]() ;
;
![]() ;
;
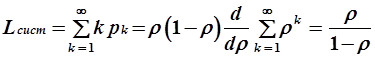 ;
;
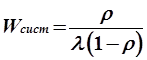 ;
; ![]() ;
;
![]() ;
; ![]() Lоч
Lоч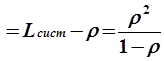 ;
;
Wоч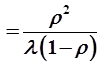
3. Одноканальная СМО с неограниченной очередью, простейшим потоком заявок и произвольным распределением времени обслуживания
На одноканальную СМО
поступает простейший поток заявок с интенсивностью l. Время обслуживания имеет
произвольное распределение с математическим ожиданием ![]() и коэффициентом вариации nm. nm — отношение среднего квадратического
отклонения времени обслуживания к его математическому ожиданию.
и коэффициентом вариации nm. nm — отношение среднего квадратического
отклонения времени обслуживания к его математическому ожиданию.
Формулы Полячека — Хинчина:
Lоч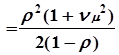 ; Lсист
; Lсист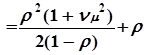
Далее, согласно формуле Литтла:
Wоч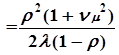 ; Wсист
; Wсист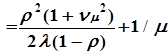
4. Одноканальная СМО с произвольным потоком заявок и произвольным распределением времени обслуживания
Рассматривается
одноканальная СМО с неограниченной очередью, на которую поступает произвольный
поток заявок с интенсивностью l и коэффициентом вариации nl, 0 < nl < 1. Время обслуживания также имеет произвольное распределение со
средним значением ![]() и коэффициентом
вариации nm, 0 < nm < 1.
Для этого случая точных аналитических формул получить не удается; можно только
приближенно оценить среднюю длину очереди, ограничить ее сверху и снизу.
и коэффициентом
вариации nm, 0 < nm < 1.
Для этого случая точных аналитических формул получить не удается; можно только
приближенно оценить среднюю длину очереди, ограничить ее сверху и снизу.
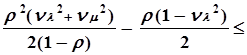 Lоч
Lоч![]()
![]()
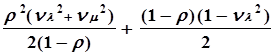
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26


