 Реферат: Расчет надежности электроснабжения подстанции Южная
Реферат: Расчет надежности электроснабжения подстанции Южная
Определим среднеквадратичное отклонение:
![]() .
.
Вычислим коэффициент вариации по формуле:
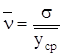 .
.
По номограмме находим значение параметра формы 1/a=0,36. По найденным значениям вычислим параметр масштаба С распределения Вейбула-Гниденко :
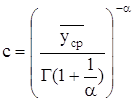
Г(1,36)=0,8902
Среднее время безотказной работы для распределения Вейбула-Гниденко определим по формуле
![]() ;
;
l2ЛЭП=1/Т2ЛЭП
В таблице 13 представлен статистический ряд восстановления отказов ЛЭП.
Интенсивность восстановления определим по формуле (1.16)
Вероятность восстановления ЛЭП определяется по формуле
Рвос.ЛЭП=1-е-m.
Таблица 13
Статистический ряд восстановления внезапных и постепенных отказов ЛЭП
|
восстановление |
|||
| 7,1 | 9,2 | 11,3 | 13,4 |
| 8,9 | 10,9 | 13 | 8,6 |
| 10,7 | 12,7 | 8,1 | 10,3 |
| 12,3 | 4,8 | 9,9 | 12,1 |
| 4,5 | 9,6 | 11,7 | 18,8 |
|
Т= |
10,395 |
m= |
0,0962 |
Результаты расчетов по приведенным выше формулам сведены в табл.11,12,13.
1.4. Модель отказов и восстановления для разъединителей
Представим разъединитель как элемент состоящий из одного элемента с внезапным отказом, с показательным законом распределения наработки на отказ (1,1). Статистический ряд представлен в таблице 14, 15 наработок на отказ и времени восстановления.
Параметр показательного закона l находим по формуле:
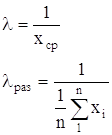
где хср— среднеее значение наработок на отказ.
Среднее время безотказной работы определим по формуле
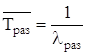
Таблица 14
Статистический ряд внезапных отказов разъединителей
|
X, г |
X, г |
X, г |
X, г |
| 6,64 | 7,40 | 6,68 | 7,13 |
| 7,06 | 7,17 | 7,44 | 7,06 |
| 6,86 | 7,12 | 7,20 | 7,22 |
| 7,20 | 6,98 | 6,83 | 7,11 |
| 6,79 | 6,83 | 7,24 | 7,48 |
|
Т=7 |
l=0,14143 |
||
Интенсивность восстановления
определим по формуле (1.16) ![]()
Вероятность восстановления разъединителей определяется:
Рвос.раз=1-е-m.
Таблица 15
Статистический ряд времени восстановления разъединителей
|
восстановление |
|||
| 8,3 | 6 | 6,2 | 7 |
| 7,5 | 8 | 8,3 | 7,2 |
| 9,1 | 9,2 | 10,9 | 9 |
| 6,8 | 10,4 | 9,4 | 8,1 |
| 10,1 | 7,1 | 8,5 | 6,1 |
|
Т=8,16 |
m=0,12255 |
||
Результаты расчетов по приведенным выше формулам сведены в табл.14,15.
1.6. Модель отказов и восстановления для отделителей и короткозамыкателей
Для отделителей и короткозамыкателей составим модель аналогичную разъединителям и проведем подобный расчет. Исходные данные и результаты расчета сведем в таблицу 16,17,18,19.
Таблица 16
Статистический ряд внезапных отказов отделителей
|
X, ч |
X, ч |
X, ч |
X, ч |
| 31377 | 35695 | 31623 | 34179 |
| 33786 | 34416 | 35974 | 33762 |
| 32653 | 34130 | 34558 | 34679 |
| 34579 | 33325 | 32455 | 34091 |
| 32231 | 32471 | 34825 | 36149 |
|
Т=33848 |
l=3E-05 |
||
Таблица 17
Статистический ряд времени восстановления отделителей
|
восстановление |
|||
| 8,1 | 5,9 | 6,1 | 6,9 |
| 7,4 | 7,8 | 8,1 | 7,1 |
| 8,9 | 9,0 | 10,6 | 8,8 |
| 6,7 | 10,2 | 9,2 | 7,9 |
| 9,9 | 7,0 | 8,3 | 6,0 |
|
Т=7,98933 |
m=0,12517 |
||


