Быстрый поиск

Реферат: Расчет надежности электроснабжения подстанции Южная

1.3. Модель отказов воздушной линии электропередач

ЛЭП рассмотрим как элемент условно состоящий из двух последовательно соединенных элементов. В одном из которых может появиться внезапный отказ, а в другом постепенный. Вероятность безотказной работы представим как произведение вероятности двух независимых событий соединенных последовательно отностительно надежности.

РЛЭП(t)=Рв(t)*Ри(t).

Дальнейший расчет проведем как и для трансформатора. Статистические данные приведенные в таблице 11 приведены к единичной длине 1 км, как для внезапных и постепенных отказов.

Таблица 11

Статистический ряд внезапных и постепенных отказов для ЛЭП

X, г	X, г	X, г	Y, г	Y, г	Y, г
174,11	203,04	179,13	309,12	326,04	343,86
180,83	41213	187,67	316,75	334,17	351,59
189,38	208,17	194,54	324,5	341,94	313,62
201,33	177,41	211,58	332,25	349,68	321,37
206,46	185,96	196,21	340,02	312,08	329,12
175,72	192,79	213,29	347,75	319,82	338,01
184,25	204,75	197,92	310,54	327,58	345,78
191,08	209,88	215,67	318,29	336,09	363,25
Т		l	Yср		Dt
1904		0,00052523	331		10

В теории надежности в качестве основного распределения времени безотказной работы при внезапных отказах ЛЭП принимается показательное распределение:

Постепенные отказы ЛЭП происходят в основном по причине износа изоляции. Износ можно описать законом распределения Вейбула-Гниденко.

где t0 — порог чувствительности, то есть элемент гарантировано не откажет, в интервале времени от 0 до t0 может быть равно нулю. Тогда окончательно имеем:

PЛЭП(t) = e-lt×e-ct=.

Параметр показательного закона l находим по формуле:

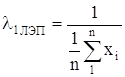
где хср— среднеее значение наработок на отказ.

Среднее время безотказной работы определим по формуле

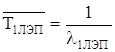
Оценим параметры распределения Вейбула-Гниденко. Для этого вычислим среднеее значение наработки на отказ

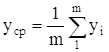
Разобьем выборку y на интервалы, которые выберем по формуле

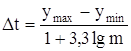
Подсчитаем сколько отказов попало в каждый из полученных интервалов

Таблица 12

интервалы	1	2	3	4	5	6
мин	309,12	318,86	328,61	338,35	348,10	357,84
макс	319	329	338	348	358	368
1	309,12	316,75	324,5	332,25	340,02	347,75
2	310,54	318,29	326,04	334,17	341,94	349,68
3	312,08	319,82	327,58	336,09	343,86	351,59
4	313,62	321,37	329,12	338,01	345,78	363,25
Yicp	311	319	327	335	343	353
pi	0,1666666	0,1666666	0,1666666	0,16667	0,16667	0,16667
D	s	n	1/a	C	T	l
199	14	0,0425237	0,035	5,7E-73	331	0,00302