 Реферат: Моделирование ЭВМ
Реферат: Моделирование ЭВМ
vihod3.dat![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 |
|||
Проверка соответствия чисел в последовательностях требуемому распределению дает следующие результаты: теоретические и статистические данные во всех 3-х файлах по критериям Колмогорова и Х2 не согласуются.
Определение числовых характеристик
| № | Характеристика | vihod1.dat | vihod2.dat | vihod3.dat |
| 1 | наименьшее значение | 0.02 | 0.005 | 0.00059 |
| 2 | наибольшее значение | 0.96 | 0.996 | 0.999 |
| 3 | Мат. ожидание | 0.39 | 0.51 | 0.49 |
| 4 | Дисперсия | 0.078 | 0.086 | 0.085 |
| 5 | Среднеквадратич.отклон. | 0.279 | 0.294 | 0.292 |
| 6 | Эксцесс | -1.92 | -1.024 | -1.12 |
Определение характеристик корреляции
![]()
![]() r(t) r(t)
r(t) r(t)

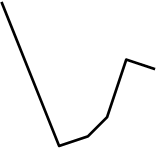 1
1
1
1
![]()
![]() 0 t
0 t
0 t
0 t
5 5
vihod1.dat vihod2.dat
![]() r(t)
r(t)
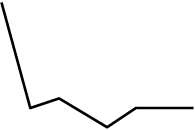 1
1
![]()
0 t
5
vihod3.dat
Вывод:
1) С увеличением числа сдвигов характеристики чисел улучшаются.
2) Из приведенных 3-ех файлов самые качественные числа находятся в
файле vihod3.dat , т. к. числа в последовательности достаточно
независимы. Но в то же время нет согласованности по обеим
критериям.
3.4.1.2. Программный способ
При программном способе псевдослучайные числа нам необходимо сформировать методом умножения.
Суть метода: выбирается два n - разрядных числа X1 и X2. X1><0, X2><0. Затем X1 умножаем на X2 и получаем некоторое значение Y , у которого 2n - разрядов: Y=X1*X2. Из 2n - разрядного Y выбираем n - разрядное Х1 и Х2 и вновь полученные Х1, Х2 умножаем друг на друга. Далее все повторяется до тех пор пока не будет сформировано необходимое количество чисел.
Программа формирования ГСК на основе метода умножения приведена в Приложении № 2.
Полученные числа записываются в файл vi_gpsc1.dat и анализируются с помощью программы analize.
Определение числовых характеристик
| № | Характеристика | Теоретич. значение | Статистич. значение |
| 1 | Мин.значение совокуп. | 0.00068 | |
| 2 | Макс.значение совокуп | 0.99995 | |
| 3 | Математич. ожидание | 0.5 | 0.4928 |
| 4 | Дисперсия | 0.083 | 0.07822 |
| 5 | Сред.квад.отклонение | 0.1887 | 0.2796 |
Аппроксимация статистического распределения теоретической функцией
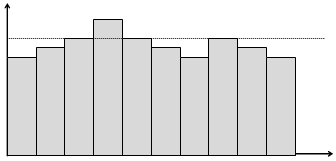
Проверка соответствия чисел последовательности требуемому распределению дает следующие результаты:
Критерий Хи-Квадрат:
Х2=12.9
С доверительной вероятностью 0.166 можно утверждать о согласованности теоретических и статистических данных.
Критерий Колмогорова:
Максимальная разность max| F(x)-F*(x) | = 0.0885
С доверительной вероятностью 0.999 можно утверждать о согласованности теоретических и статистических данных.
Определение характеристик корреляции
r(t)
![]()
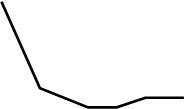 1
1
![]() 0 t
0 t
5
Рис. 3. График изменения коэфф.
корреляции
Вывод:
Полученная по методу умножения последовательность СЧ, имеющих равномерный закон распределения удовлетворяет предъявленным требованиям по качеству и может быть использован в задачах моделирования, т. к.:
1) есть согласованность по критерию Колмогорова
2) числа не зависят друг от друга, о чем говорит график (Рис. 3.)
3.4.1.3. Выбор генератора РРПСЧ
Эффективность статистического моделирования и достоверность полученных результатов находятся в прямой зависимости от качества используемых в модели случайных последовательностей. Под качеством здесь понимается соответствие чисел последовательности заданной функции распределения (плотности распределения) и ее параметрам: М.О. и т.д.; независимость чисел последовательности друг от друга, т.е. отсутствие автокорреляции в последовательности случайных чисел.
Выберем генератор РРПСЧ, который используется для генерации времени между поступлениями заявок от пользователей.
Последовательность чисел, полученных аппаратным способом и хранящихся в файле vihod3.dat не совсем удовлетворяет предъявленным требованиям по качеству, т.к. нет согласия по критериям теоретических и статистических данных.
В пункте 3.4.1.2. мы делая вывод уже говорили о том, что генератор РРПСЧ сформированный программным способом (по методу умножения) можно использовать в задачах моделирования, но для простоты будем использовать встроенную функцию random( ), простую в программировании и имеющую хорошие характеристики.
3.4.2. Моделирование случайных воздействий,
имеющих неравномерное распределение
Для стохастической модели требуются числа распределенные по нормальному закону и по экспоненциальному закону.


