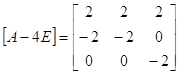Реферат: Матричный анализ
Реферат: Матричный анализ
Теорема. Алгебраическая кратность собственного значения не меньше его геометрической кратности.
DF.
Матрица ![]() называется простой, если аглебраическая
кратность каждого ее собственного значения совпадает с его геометрической
кратностью.
называется простой, если аглебраическая
кратность каждого ее собственного значения совпадает с его геометрической
кратностью.
Из
линейной алгебры следует, что матрица ![]() простая
тогда и только тогда, когда
простая
тогда и только тогда, когда ![]() .
.
Если
матрица А простая, тогда существует n линейно независимых собственных
векторов x1, x2,
…,xn таких, что ![]() , для
, для ![]() . Запишем это равенство в
матричном виде:
. Запишем это равенство в
матричном виде:
![]()
![]() ,
т.е. А – простая тогда и только тогда, когда
,
т.е. А – простая тогда и только тогда, когда ![]() и
и
![]() .
.
Замечание. Обратим
внимание на то, что собственные значения А и А’ совпадают.
Действительно, собственные значения для А’ это значения ![]() . Таким образом
характеристические многочлены матриц совпадают. Размерность
. Таким образом
характеристические многочлены матриц совпадают. Размерность ![]() , тогда
, тогда ![]() . Поэтому, если
. Поэтому, если ![]() - собственное значение
матрицы А, то и
- собственное значение
матрицы А, то и ![]() является
собственным значением матрицы А’, т.е. существует
является
собственным значением матрицы А’, т.е. существует ![]() ,
что
,
что ![]() (*) или
(*) или ![]() .
Транспонируем (*) и получим
.
Транспонируем (*) и получим ![]() (транспонируем это
равенство). В этом случае
(транспонируем это
равенство). В этом случае ![]() называют
левым собственным вектором матрицы А. Соответственно,
называют
левым собственным вектором матрицы А. Соответственно, ![]() - называют правым
собственным подпространством,
- называют правым
собственным подпространством, ![]() - называют левым собственным
подпространством.
- называют левым собственным
подпространством.
Рассмотрим
следующую конструкцию: если матрица А простая, то существует n
линейно независимых собственных векторов x1, x2, …, xn и существует n линейно
независимых собственных векторов y1,
y2,…,yn, где x1, x2, …, xn такие, что ![]() ,
, ![]() (1); y1,
y2,…,yn такие, что
(1); y1,
y2,…,yn такие, что ![]() (2),
(2), ![]() .
.
Запишем
равенство (1) в виде ![]() (3) Þ что, если А – простая, то существуют матрицы X и Y, что
(3) Þ что, если А – простая, то существуют матрицы X и Y, что ![]() или
или
![]() (**).
(**).
DF. Множества векторов x1, x2, …, xn и y1,
y2,…,yn удовлетворяющие условию 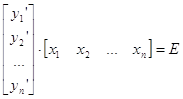 , т.е.
, т.е. ![]() называются
квазиортогональными.
называются
квазиортогональными.
Учитывая
равенство (**) и определение делаем вывод: множества левых и правых собственных
векторов простой матрицы А квазиортогональны и ![]() .
.
Очень важной для матриц является следующая теорема:
СПЕКТРАЛЬНАЯ ТЕОРЕМА.
Если А – простая матрица порядка n над полем С и p(x) многочлен
из кольца C[x], и x1,
x2, …, xn и y1, y2,…,yn
– множества правых и левых собственных векторов
матрицы А, то ![]() , а сопутствующая
матрица
, а сопутствующая
матрица ![]() , где
, где ![]() .
.
Следствие. Сопутствующие матрицы обладают следующими свойства:
1.
![]()
2.
![]()
3.
![]()
Пример.
Показать, что матрица ![]() простая. Найти
сопутствующие матрицы для матрицы А и использовать их для А20, p(x)=x20.
простая. Найти
сопутствующие матрицы для матрицы А и использовать их для А20, p(x)=x20.
Решение:
![]()
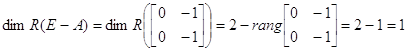
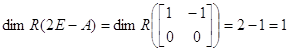 Þ
Þ
существуют 2 линейно независимые правые и левые системы собственных векторов.
Найдем правые собственные векторы:
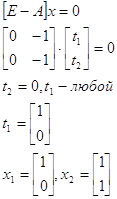
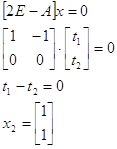
Найдем левые собственные векторы:
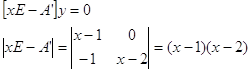
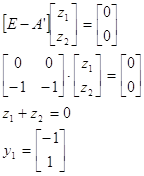
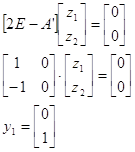
Найдем сопутствующие матрицы:
![]()
![]()
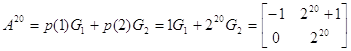 .
.
5.Спектральное разложение функции f(A).
Спектральное разложение для f(A) имеет важное значение и очевидно тесно примыкает к спектральной теореме для простых матриц.
Пусть
дана матрица ![]() и пусть
и пусть ![]() ,
, ![]() .
.
Теорема. Если ![]() , а функция f(x) определена
на спектре матрицы А и
, а функция f(x) определена
на спектре матрицы А и ![]() - значение j-й
производной от f(x) в собственном значении
- значение j-й
производной от f(x) в собственном значении ![]() ,
где
,
где ![]() ,
, ![]() , то существуют такие
независимые от f(x) матрицы
, то существуют такие
независимые от f(x) матрицы ![]() , что (1)
, что (1) ![]() ,
при чем
,
при чем ![]() коммутирует с матрицей А и
образуют линейно независимую систему в пространстве
коммутирует с матрицей А и
образуют линейно независимую систему в пространстве ![]()
Доказательство: заметим, что ![]() и
и
![]() , где
, где ![]() - базисные многочлены,
принимающие одинаковые значения на спектре матрицы А,
- базисные многочлены,
принимающие одинаковые значения на спектре матрицы А, ![]() (3). Сравнивая (1) и (2) и учитывая (3) получим, что
(3). Сравнивая (1) и (2) и учитывая (3) получим, что ![]() . Матрицы
. Матрицы ![]() называются компонентами
матрицы А или компонентными матрицами.
называются компонентами
матрицы А или компонентными матрицами.
ЧТД.
Опишем следующие свойств компонентных матриц, которые в некоторой степени обобщают свойства сопровождающих матриц.
Теорема. Компонентные
матрицы ![]() обладают следующими
свойствами:
обладают следующими
свойствами:
1.
![]()
2.
![]()
3.
![]()
4.
![]() .
.
Замечание. Для того, чтобы найти компонентные матрицы для f(x) определенной на спектре матрицы А необходимо и достаточно знать базисные многочлены, входящие в интерполяционный многочлен, однако нахождение интерполяционного многочлена f(x) связано с некоторыми трудностями, а поэтому будем вычислять компонентные матрицы подбирая соответствующим образом системы функций.
Пример:
Найти компоненты для матрицы 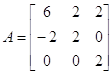 .
.
![]() .
.
Пусть
f(x) определена на спектре А, тогда согласно спектральной
теореме ![]() .
.
1. f(x)=1
E=1Z11+0Z12+1Z21=Z11+Z21
2. f(x)=x-4
A-4E=0Z11+1Z12+(-2)Z21=Z12-2Z21
3. f(x)=(x-4)2
(A-4E)2=4Z21