 Реферат: Математичекие основы теории систем: анализ сигнального графа и синтез комбинационных схем
Реферат: Математичекие основы теории систем: анализ сигнального графа и синтез комбинационных схем
2.2 Составление логических функций
Существует два способа записи логической функции по таблице истинности: запись дизъюнктивной совершенной нормальной формы (ДСНФ) и запись конъюнктивной совершенной нормальной формы (КСНФ). В первом случае образуют дизъюнкции, соответствующие входным наборам, на которых функция принимает значение «1», их объединяют знаками конъюнкции. Во втором случае организуют конъюнкции, соответствующие входным словам, на которых функция принимает значение «0», эти конъюнкции объединяют знаками дизъюнкции. Рассмотрим на примере функции у3.
2.2.1 Дизъюнктивная совершенная нормальная форма
Введем понятие логической
степени, которою будем обозначать ![]() . Тогда,
логическая степень будет определяться по формуле (2.1)
. Тогда,
логическая степень будет определяться по формуле (2.1)
![]() (2.1)
(2.1)
Любую функцию от n переменных можно представить в виде (см.(2.2))
![]() (2.2)
(2.2)
![]() означает, что коллективные
члены формируются только для таких наборов (α1, α2,…,
αn) для которых функция принимает
единичное значение.
означает, что коллективные
члены формируются только для таких наборов (α1, α2,…,
αn) для которых функция принимает
единичное значение.
Форма (2.2) определяет алгоритм перехода от таблицы истинности к аналитическому ее виду. Для такого перехода используется следующий алгоритм:
а) Выбрать в таблице истинности все наборы, в которых функция обращается в единицу.
б) Выписать конъюнкции, соответствующие этим наборам аргументов. При этом если аргумент хi входит в данный набор как «1», то он вписывается без изменения в конъюнкцию, соответствующую данному набору. Если же входит в данный набор как «0», то в соответствующую конъюнкцию вписывается его отрицание.
в) Все полученные конъюнкции объединяют знаком дизъюнкции.
Для функции у3 СДНФ будет иметь вид:
![]()
2.2.2 Конъюнктивная совершенная нормальная форма
Любую функцию от n переменных можно представить в виду:
f= ![]()
![]() означает, что коллективные члены
формируются только для таких наборов, (α1, α2,
…, αn) для которых функция принимает
нулевое значение.
означает, что коллективные члены
формируются только для таких наборов, (α1, α2,
…, αn) для которых функция принимает
нулевое значение.
Следующий алгоритм позволяет перейти от табличной записи функции к СКНФ:
а) Выбрать в таблице истинности все наборы, в которых функция обращается в «0».
б) Выписать дизъюнкции, соответствующие этим наборам аргументов. При этом если аргумент хi входит в данный набор как «0», то он вписывается без изменения в дизъюнкцию, соответствующую данному набору. Если же входит в данный набор как «1», то в соответствующую дизъюнкцию вписывается его отрицание.
в) Все полученные дизъюнкции объединяют знаком конъюнкции
Функция У3 в виде СКНФ будет иметь вид:
![]()
2.3 Минимизация булевых функций
Минимизация сводится к поиску минимальных форм (ДНФ и КНФ). Минимальной форме соответствует самая простая логическая схема, реализующая данную функцию и требующая минимальных аппаратных затрат.
В ходе курсового проектирования была выполнена минимизация полученных булевых функций следующими методами:
1. метод неопределенных коэффициентов
2. метод Квайна-Мак-Класки
3. карты Карно
Для примера в курсовом проекте рассмотрена минимизация этими способами для функции y3.
2.3.1 Пример минимизации методом неопределенных коэффициентов
Данный метод является по своим идеям наиболее простым. Для функции записываются все возможные конъюнктивные члены, которые могут входить в дизъюнктивную форму представления функции. Коэффициенты К с различными индексами являются неопределенными и подбираются так, чтобы получающаяся после этого дизъюнктивная форма была минимальной.
Если теперь задавать всевозможные наборы значений аргументов и приравнивать полученное после этого выражение значению функции на выбранных наборах, то получим систему 24 уравнений для определения коэффициентов К:
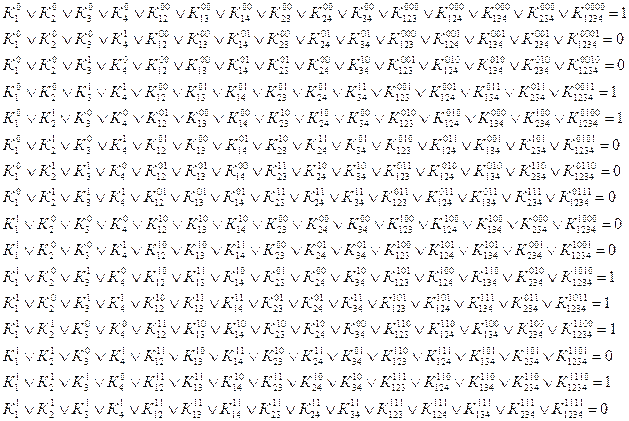
Находим выражения, имеющие в правой части ноль. Исходя из определения дизъюнкции вычеркиваются все элементы в этих уравнениях и эти же элементы находящиеся в других уравнениях. В итоге получим уравнения:
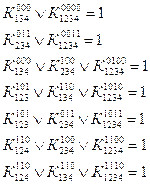
Из оставшихся коэффициентов приравниваем единице коэффициент, определяющий конъюнкцию наименьшего возможного ранга, а остальные коэффициенты в левой части данного уравнения приравняем нулю(это можно сделать, так как дизъюнкция обращается а единицу, если хотя бы один член ее равен единице). Тогда уравнения примут вид:
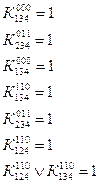
![]()
2.3.2 Пример минимизации методом Квайна-Мак-Класки.
При минимизации по данному методу предполагается, что минимизируемая функция задана в СДНФ. Метод Квайна – Мак – Класки состоит из последовательного выполнения следующий этапов.
Метод Квайна состоит из последовательного выполнения этапов:
1) Нахождение первичных импликант
2) Расстановка меток
3) Нахождение существенных импликант
4) Вычеркивание лишних столбцов
5) Вычеркивание лишних
6) Получение минимального покрытия
Выполним, приведенные этапы, для функции У3.
Нахождение первичных импликант. Все минитермы (элементарные конъюнкции, входящие в ДНФ) данной функции записываются в виде их двоичных номеров. Все номера разбиваются по числу единиц в этих номерах на не пересекающиеся группы. При этом в i-тую группу войдут все номера, имеющие в своей двоичной записи ровно i единиц. По парное сравнение (склеивание) можно производить только между соседними по номеру группами. При образовании минитермов с рангом выше нулевого в разряды, соответствующие исключенным переменным, пишется знак тире. Минитермы, не склеивающиеся между собой, называются первичными импликантами.
СДНФ, которую мы нашли ранее, для функции У3 имеет вид:
![]()
Составим минитермы для этой функции:
Таблица 2.2.1
|
Минитермы длиной 4 |
Минитермы длиной 3 |
||
|
Нулевая группа |
0000+ |
Нулевая группа |
0-00 |
|
Первая группа |
0100+ |
Первая группа |
-100, -011 |
|
Вторая группа |
1100, 1010, 0011 |
Вторая группа |
11-0, 1-10, 101- |
|
Третья группа |
1110, 1011 | ||
Расстановка меток. Остальные этапы нужны, чтобы отбросить некоторые первичные импликанты. На данном этапе составляется таблица, число строк которой равно числу полученных первичных импликант, число столбцов совпадает с числом минитермов СДНФ. Если в некоторый минитерм СДНФ входит какая – либо из первичных импликант, то на пересечении соответствующего столбца и строки ставится метка. В таблице 2.2.2 приведем результат расстановки меток:
Таблица 2.2.2
|
0000 |
0100 |
1100 |
1010 |
0011 |
1110 |
1011 |
||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 |
0-00 |
У | У | |||||
| 2 |
-100 |
У | У | |||||
| 3 |
-011 |
У | У | |||||
| 4 |
11-0 |
У | У | |||||
| 5 |
1-10 |
У | У | |||||
| 6 |
101- |
У | У |
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10


