Реферат: Математичекие основы теории систем: анализ сигнального графа и синтез комбинационных схем
Для x1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Для x4
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Для y
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 6 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Для x13
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 6 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
1.9 Формула Мэзона для заданного сигнального графа
Используя универсальную топологическую формулу, носящую имя Мэзона, можно получить передачу между любыми двумя вершинами. Формула имеет следующий вид:
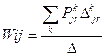
где 
-
передача k-го пути между вершинами j и r; 
D - определитель
графа. Он характеризует контурную часть графа и имеет следующий вид:
где, L – множество индексов контуров, L2 - множество пар индексов
не касающихся контуров, L3 - множество троек индексов
не касающихся контуров, Ki – передача i-го контура, 
- минор пути, это
определитель подграфа, полученного удалением из полного графа вершин и дуг,
образующих путь 
.
D=1-К1-К2-К3-К4-К5-К6-К7-К8+К7К2+К7К3+К7К5+К7К6+К7К8=1- К1-К2-К3-К4-К5-К6-К7-К8+К7(К2+К3+К5+К6+К8)
К1=W1W3W4W5W6
K2=W3W4W7
K3=W1W3W4W8
K4=W2W3W4W6 W7
K5=W2W3W4W7
K6=W2W3W4W8
K7=W5W6
K8=W3W4
D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1)
Для x1
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
