Реферат: Контрольная работа

3. Построить линейную модель , параметры которой оценить МНК.

Определим  и

 ;

;

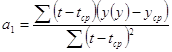т.о. линейная модель имеет вид:

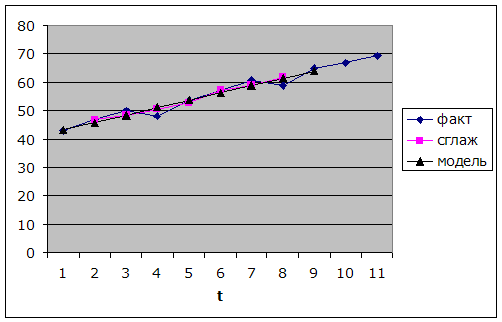
Последовательно подставляя в линейную модель вместо  его значения от 1 до 9 получим расчетные значения уровня :

;              

;             

;              

;                

                  

Вычислим отклонения расчетных значений от фактических:

,

затем результаты запишем таблицу.

5. Оценить адекватность модели на основе исследования:

a) случайности остаточной компоненты по критерию пиков

		Поворотные точки
1	-0,4	-
2	1	0
3	1,4	1
4	-3,2	0
5	0,2	0
6	0,6	0
7	2	1
8	-2,6	0
9	0,8	-

Общее число пиков p=2

; ;

Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства , т.о. имеем:

,

следовательно, свойство случайности не выполняется, трендовая модель является неадекватной.

б) независимости уровней ряда остатков по  - критерию (в качестве критических используйте уровни  и ) или по первому коэффициенту корреляции, критический уровень которого .

Проверка независимости уровней остаточной последовательности осуществляется по формуле Дарбина-Уотсона:

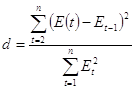, имеем:

	0,16	-	-	-
	1	1,4	1,96	-0,4
	1,96	0,4	0,16	1,4
	10,24	-4,6	21,16	-4,48
	0,04	3,4	11,56	-0,64
	0,36	0,4	0,16	0,12
	4	1,4	1,96	1,2
	6,76	-4,6	21,16	-5,2
	0,64	3,4	11,56	-2,08
	25,16		69,68	-10,08

т.к.  , то имеет место отрицательная связь, преобразуем значения :

; ; ;

Сравним  с  и , Т.к. , то нет достаточных оснований сделать вывод об адекватности модели.

в) нормальности закона распределения остаточной последовательности по RS-критерию с критическими уровнями 2,7-3,7.

, где , т.о. имеем:

 и

Расчетное значение RS-критерия равное 2,9 попадает внутрь [2,7-3,7], т.о. гипотеза о соответствии распределения остаточной компоненты нормальному закону распределения принимается.

г) Для оценки точности модели используйте среднее квадратическое отклонение и среднюю ошибку по модулю.

Т.к. модель неадекватна, то нет смысла говорить о ее точности.

6. Постройте точечный и интервальный прогнозы на два шага вперед.

Точечный прогноз на K шагов вперед получается путем подстановки в модель . При прогнозировании на два шага имеем:

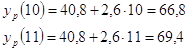
Доверительный интервал прогноза будет иметь следующие границы:

Верхняя:

Нижняя:

Величина  для линейной модели имеет вид:

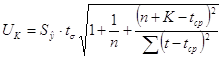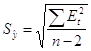, где , т.о. имеем:

;

	Шаг,	Прогноз,	Нижняя граница,	Верхняя граница,
10	1	66,8	61,4	72,2
11	2	69,4	63,7	75,1

Тема 9.

Даны коэффициенты прямых поставок  и конечный продукт . Требуется:

1)   Определить межотраслевые поставки продукции

2)   Проверить продуктивность матрицы A

Отрасли	Коэффициенты прямых поставок,			Конечный продукт,
	1	2	3
1	0,0	0,1	0,2	180
2	0,1	0,2	0,1	200
3	0,2	0,1	0,2	200

            1) ;

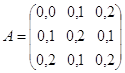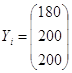
            Найдем , где - матрица коэффициентов полных материальных затрат.

           

            2)

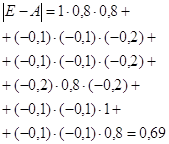
            3)

            ;       

            ;      

            ;      

            ;      

           

   ;

   ;

      ;

      ;

      ;

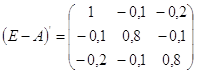
      т.о.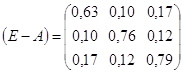

      5)

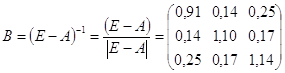
      Диагональные элементы матрицы строго больше нуля.

      Определим межотраслевые поставки:

      ;

     

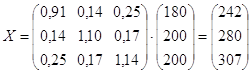
      Находим матрицу межотраслевых поставок продукции:

      ;

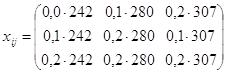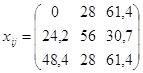
	1	2	3		Валовой продукт
1	0	28	61,4	180	242
2	24,2	56	30,7	200	280
3	48,4	28	61,4	200	307
Условно чистый продукт	266,2	336	337,7	580
Шахматный баланс	242	280	307

3)   Матрица продуктивна, если норма матрицы (наибольшая сумма по столбцам)

Норма матрицы , т.о. матрица  продуктивна.