Реферат: Дискретно-аналоговое представление
, при 
(23)
, при 
, 
(24)
На практике интерполяция по Лагранжу используется при n = 1, 2, 3:
1. Ступенчатая интерполяция (полиномы нулевой степени ) (рисунок 9).
В этом случае n = 1 и для интерполяции используется лишь одна выборка
, 
, 
и 
.
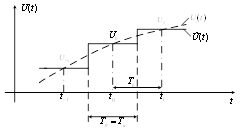
Рисунок 9
2. Линейная интерполяция (полиномы первой степени) (рисунок 10).
При
этом 
, 
, 
и
интерполирующие функции имеют вид
, 
.
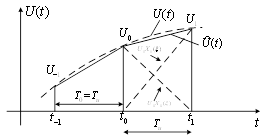
Рисунок 10
3. Квадратичная интерполяция (квадратичная интерполяция) (рисунок 11).
При
этом 
, 
, 
и
интерполирующие функции имеют вид
, 
, 
.
Рисунок 11
Можно показать, что верхние оценки относительных ошибок в этом случае равны
, 
, 
,
где
-
граничная частота спектра сигнала, 
- частота опроса.
При
и 
частота опроса
, 
, 
.
При
восстановлении функции по отсчетам обычно получается плавная кривая, поэтому,
можно для практических расчетов выбрать частоту опроса по формуле 
.
Определим
частоту опроса первичного сигнала при среднем квадратическом приближении алгебраическими
полиномами. Используем показатель верности оценки 
в форме интегральной средней
квадратической ошибки
. (26)
Более удобно использовать приведенный показатель верности:
. (27)
Применим эту формулу для определения частоты опроса четырех моделей первичного сигнала:
Модель 1. Сигнал с ограниченным равномерным спектром (рисунок 12).
Рисунок 12
Применяя
косинус преобразование Фурье от 
, получим функцию корреляции этого
сигнала:
. (28)
Модель 2. Сигнал с треугольным спектром (рисунок 13).
, 
.
Рисунок 13
Эффективная ширина спектра в этом случае имеет вид
,
а функция корреляции равна
. (29)
Модель 3. Сигнал марковского типа (рисунок 14).
Энергетический спектр этого сигнала описывается соотношением
,
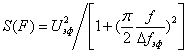а функция корреляции равна
. ( 30)
Рисунок 14
Модель 4. Сигнал с колокольным спектром (рисунок 15).
Энергетический спектр этого сигнала описывается соотношением
,
где
,
а функция корреляции равна
. (31)
Рисунок 15
Эти
модели охватывают значительную часть практически используемых сигналов и
являются стационарными случайными процессами. Применяя для этих моделей
интерполяцию по Лагранжу при 
получим следующие формулы
(таблица 1) для расчета величины æ = 
.
В
случае модели 1 и идеальной интерполяции, т.е. при опросе по В.А. Котельникову,
æ = 1. Формулы, приведенные в таблице используются для определения
частоты опроса 
= æ
.
Таблица 1
| Модель |
æ
= |
||
| 1 | n = 1 | n = 2 | n = 3 |
|
|
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
Построим
графики зависимости æ от показателя верности 
для различных моделей сигналов
(рисунки 16, 17).
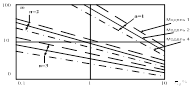
Рисунок 16
Рисунок 17
Заключение
Для всех моделей, за исключением третьей, интерполяция полиномами более высокого порядка позволяет уменьшить частоту опроса при той же верности.
1. При
переходе от линейной интерполяции к квадратичной, уменьшение частоты опроса 
не столь
значительно, как при переходе от ступенчатой интерполяции к линейной.
2. Увеличивать степень полинома целесообразно только при увеличении требований к точности интерполяции.
3. Для третьей модели переход от линейной модуляции к квадратичной нецелесообразен, что объясняется свойствами марковских сигналов.
4. При интерполяции алгебраическими полиномами первичного сигнала коэффициент корреляции между соседними выборками равен 0,85 – 0,995. Это приводит к неэффективному использованию пропускной способности канала передачи информации.
5. Для определения частоты опроса необходимо располагать:
- спектральными
характеристиками первичного сигнала, т.е. полосой 
по уровню 0,99 энергии сигнала;
- точностными
характеристиками, т.е. показателем верности 
%;
- задать алгоритм обработки, т.е. тип интерполирующего полинома.
Список литературы:
1. Радиотехнические методы передачи информации: Учебное пособие для вузов / В.А. Борисов, В.В. Калмыков, Я.М. Ковальчук и др.; Под ред. В.В. Калмыкова. М.: Радио и связь. 1990. 304с.
2. Системы радиосвязи: Учебник для вузов / Н.И. Калашников, Э.И. Крупицкий, И.Л. Дороднов, В.И. Носов; Под ред. Н.И. Калашникова. М.: Радио и связь. 1988. 352с.
3. Тепляков И.М., Рощин Б.В., Фомин А.И., Вейцель В.А. Радиосистемы передачи информации: Учебное пособие для вузов / М.: Радио и связь. 1982. 264с.
4. Кириллов С.Н., Стукалов Д.Н. Цифровые системы обработки речевых сигналов. Учебное пособие. Рязань. РГРТА, 1995. 80с.
5. Кириллов С.Н., Бакке А.В. Оптимизация сигналов в радиотехнических системах. Учебное пособие. Рязань. РГРТА, 1997. 80с.
6. Кириллов С.Н., Шелудяков А.С. Методы спектральной обработки речевых сигналов. Учебное пособие. Рязань. РГРТА, 1997. 80с.
