Быстрый поиск

Реферат: Дискретно-аналоговое представление

Содержание

Введение

1. Дискретно-аналоговое представление регулярными выборками

2. Физическая трактовка процессов интерполяции сигналов

3. Задачи идеальной интерполяции

4. Интерполяция алгебраическими полиномами

5. Определение частоты опроса

Заключение

Список литературы

Введение

В первой половине ХХ века при регистрации и обработке информации использовались, в основном, измерительные приборы и устройства аналогового типа, работающие в реальном масштабе времени, при этом даже для величин, дискретных в силу своей природы, применялось преобразование дискретных сигналов в аналоговую форму. Положение изменилось с распространением микропроцессорной техники и ЭВМ. Цифровая регистрация и обработка информации оказалась более совершенной и точной, более универсальной, многофункциональной и гибкой. Мощь и простота цифровой обработки сигналов настолько преобладают над аналоговой, что преобразование аналоговых по природе сигналов в цифровую форму стало производственным стандартом.

Под дискретизацией сигналов понимают преобразование функций непрерывных переменных в функции дискретных переменных, по которым исходные непрерывные функции могут быть восстановлены с заданной точностью. Роль дискретных отсчетов выполняют, как правило, квантованные значения функций в дискретной шкале координат. Под квантованием понимают преобразование непрерывной по значениям величины в величину с дискретной шкалой значений из конечного множества разрешенных, которые называют уровнями квантования. Если уровни квантования нумерованы, то результатом преобразования является число, которое может быть выражено в любой числовой системе. Округление с определенной разрядностью мгновенных значений непрерывной аналоговой величины с равномерным шагом по аргументу является простейшим случаем дискретизации и квантования сигналов при их преобразовании в цифровые сигналы.

Как правило, для производственных задач обработки данных обычно требуется значительно меньше информации, чем ее поступает от измерительных датчиков в виде непрерывного аналогового сигнала. При статистических флюктуациях измеряемых величин и конечной погрешности средств измерений точность регистрируемой информация также всегда ограничена определенными значениями. При этом рациональное выполнение дискретизации и квантования исходных данных дает возможность снизить затраты на хранение и обработку информации.

Кроме того, использование цифровых сигналов позволяет применять методы кодирования информации с возможностью последующего обнаружения и исправления ошибок при обращении информации, а цифровая форма сигналов облегчает унификацию операций преобразования информации на всех этапах ее обращения.

1. Дискретно-аналоговое представление регулярными выборками

При дискретно-аналоговом представлении сообщение на интервале времени T описывается вектором

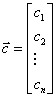, (1)

где - координаты.

Если шкала каждой координаты непрерывная, то это представление называется дискретно-аналоговым, а если шкала квантованная, то представление дискретно-квантованное, т.е. цифровое.

Дискретно-аналоговое представление сообщений может быть реализовано различными способами в зависимости от выбора системы координат. Наибольшее применение в РСПИ получили представления, у которых в качестве координат сообщения используется текущее значение сигнала в фиксированные моменты времени.

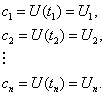(2)

Координаты называются выборками или отсчетами, а моменты времени - точками опроса.

При представлении регулярными выборками расстояние между соседними точками опроса одинаково и равно .

, (3)

где - период опроса, - частота опроса.

Частота опроса является важнейшим параметром, который надо выбирать при представлении сообщения регулярными выборками.

Процесс формирования выборок в этом случае изображен на рисунке 1:

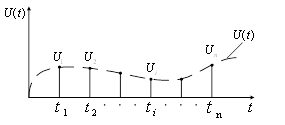
Рисунок 1

Выбор частоты опроса зависит от способа восстановления исходного сообщения на приемном конце. Восстановление непрерывной функции по её выборкам называется интерполяцией.

Рассмотрим случай, когда потребителю необходимо восстановить на приёмной стороне функцию. Реально при восстановлении функции может быть получена только её оценка . Для доказательства этого утверждения представим интерполяционную обработку в следующем виде:

, (4)

где - интерполирующая (восстанавливающая, синтезирующая) функция. Функция

, (5)

т.е. есть функция с началом отсчета в точкемер выборки первичного сигнала. Суммирование в выражении (4) ведется по всем выборкам, участвующим в обработке. Определение вида функции составляет сущность задачи выбора способа интерполяционной обработки.

На точность функции восстановления функции влияют следующие факторы:

- шумы интерполяции;

- шумы радиолинии;

- погрешности системы.

В дальнейшем будем учитывать только ошибку за счет интерполяции. Т.е. выборки будут считаться точными, а шумы отсутствующими. Тогда выражение для оценки первичного сигнала будет иметь следующий вид:

. (6)

Ошибка интерполяционной обработки в этом случае равна:

. (7)

При этом оценка должна быть получена на некотором интервале интерполяции с учетом выборок, расположенных на конечном интервале обработки . Интервал обработки должен последовательно перемещаться в пределах интервала наблюдения (рисунок 2).

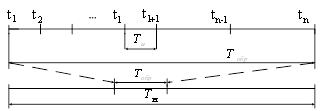
Рисунок 2

Таким образом, функция должна быть восстановлена для всех значений времени, лежащих внутри интервала интерполяции , путем использования выборок в моменты времени .Это возможно потому, что существует корреляционная зависимость между значением первичного сигнала , моментами времени и . Интерполяция белого шума невозможна, т.к. его корреляционная функция есть дельта – функция.

Теоретически необходимо учитывать все отсчеты на интервале наблюдения , т.е. полагать = . Но при этом результаты интерполяции могут быть получены спустя время , и для реализации требуется устройство с большой памятью. С удалением точки опроса от интервала интерполяции уменьшаются корреляционные связи и их учет дает малый вклад в ошибку интерполяции. Поэтому имеют смысл учитывать только те отсчеты, выборки которых коррелированны с функцией на интервале интерполяции , с коэффициентами корреляции К(τ) = 0.05 – 0.2. Конкретные значения К(τ) определяются требованиями к точности интерполяции.