Реферат: Цифровая обработка сигнала (Digital Signal processing)

- Авто корреляционный метод.

Модель такая: минимизируется ошибка следующим образом:

                           

а – коэффициент линейного предсказания.

R – авто корреляционная матрица.

r – коэффициенты матрицы.

 

                                     

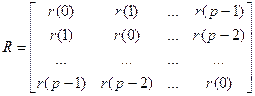
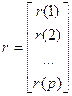
Эта модель сводится к модели фильтрации сигналов и будет:

  

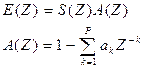
S(Z) - Z–преобразование сигнала

A(Z) – фильтр (анализатор) сигнала

Любая модель линейного предсказания приводит к ошибкам предсказания. В случае, если мы используем авто корреляционный метод, тогда ошибка предсказания будет:

     

                                  

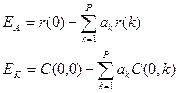
Тема: Цифровая обработка сигналов.

1)    Достоинства методов цифровой обработки сигналов.

2)    Линейные и дискретные системы и их свойства.

3)    Цифровые фильтры и способы их описания.

4)    Фильтры с конечно импульсными характеристиками.

5)    Фильтры с бесконечно импульсными характеристиками.

6)    Передаточные характеристики фильтров.

7)    Нули и полюса фильтров.

8)    Фильтры первого порядка с одним нулем и с одним полюсом.

9)    Фильтры второго порядка с нулями и плюсами.

10)  Топология фильтров.

I. Достоинства ЦОС.

1. Экономное использование средств для обработки сигналов.
2. Гибко использовать программные средства для обработки сигналов различными методами.
3. Цифровые способы обработки сигналов не зависят от внешних условий.
4.  Цифровые способы позволяют моделировать любые устройства с необходимыми характеристиками.

II. Цифровая обработка сигналов использует линейные дискретные системы, которые наиболее проще описывают те процессы, которые протекают при обработке сигналов.

Свойства:

1. Однородности:

ЛС

X                          Y                    

2. Суперпозиции:                  X1                                                                                        

                                                 X2                      Y1+Y2                   

                                                                               

3. Инвариантности:                   Т – любая.

Если минимальные системы подчиняются свойствам выше, тогда их работу можно описать с помощью измерения импульсных откликов на входах и выходах этих систем.

ЛС

                                            =1    для n = 0

                                                              =0    для n0

Исходя из этих свойств, входной сигнал Х(n) можно представить как сумму отчетов дискритизированного сигнала умноженную на…

 

 - цифровая свертка.

III. Цифровые фильтры.

Фильтры можно получить, используя линейные комбинации предыдущих и текущих отчетов сигналов.

С точки зрения характеристик фильтра на единичный конечный сигнал, имеются фильтры с конечно импульсными характеристиками (КИХ) и с бесконечно импульсными характеристиками (БИХ).

	Z-1

IV. Простейший пример КИХ.

              

Схема этого фильтра выглядит следующим образом:

 

               X(n)                                                                        Y(n)                            

 

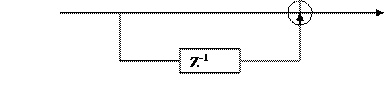
Фильтр и КИХ в общем виде описывается следующим образом:

                               X(1)

Z-1

Z-1

Z-1

Z-1

                                                      

Данный фильтр является неимпульсивным, и значение выходного сигнала зависит только от значений входного сигнала и от предыдущих значений.

V. Фильтры с БИХ.

Фильтры с БИХ математически списываются следующим образом:

                   

для g=1

тогда импульсный отклик будет rn.

Этот тип отклика называется экспонициальный.

Если r 0, тогда даже при нулевом значении входного сигнала, выходной сигнал не будет нулевым.

Если r < 1, тогда выходное значение сигнала на выходе фильтра будет осцелировать.

Если r > 1, выходное значение может бесконечно расти, то тогда этот фильтр будет неустойчивый, и приходим к выводу, что эти фильтры называются «с бесконечно импульсными характеристиками».

Схема такого фильтра выглядит следующим образом:

                 X(n)                                                   Y(n) 

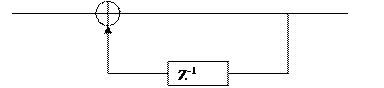
Этот фильтр еще называется рекуррентный фильтр с БИХ первого порядка.

Схема фильтра n – го порядка выглядит следующим образом:

                       X(n)                                                     Y(n) 

Общая форма фильтров:

 

 

Если использовать Z–преобразования, тогда фильтр можно описать следующей формулой:

Страницы: 1, 2, 3, 4, 5, 6