Курсовая работа: Задача о коммивояжере и ее обобщения
выбор индивидов из текущей популяции (селекция);
скрещивание и\или мутация;
вычисление функций полезности для всех особей;
формирование нового поколения;
если условия совпали, то решение найдено (конец цикла), если нет, то цикл повторяется.
Применяются генетические алгоритмы для решения следующих задач:
оптимизация функций, разнообразные задачи на графах (задача коммивояжера, раскраска, нахождение паросочетаний), настройка и обучение искусственной нейронной сети, задачи компоновки, составление расписаний, игровые стратегии, аппроксимация функций, искусственная жизнь, биоинформатика (свёртывание белков).
4. NP-ПОЛНАЯ ЗАДАЧА
Все эффективные (сокращающие полный перебор) методы решения задачи коммивояжёра — методы эвристические («жадные алгоритмы»). В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы так называемые any-time алгоритмы, то есть постепенно улучшающие некоторое текущее приближенное решение.
Задача коммивояжёра есть NP-полная задача. Часто на ней проводят обкатку новых подходов к эвристическому сокращению полного перебора.
В теории алгоритмов NP-полные задачи — это класс задач, лежащих в классе NP (то есть для которых пока не найдено быстрых алгоритмов решения, но проверка того, является ли данное решение правильным, проходит быстро), к которым сводятся все задачи класса NP.
Назовём языком множество слов над алфавитом Σ. Задачей здесь является определение того, принадлежит данное слово языку или нет. Язык L1 называется сводимым (по Карпу) к языку L2, если существует функция, вычислимая за полиномиальное время, обладающая следующим свойством: f(x) принадлежит L2 тогда и только тогда, когда x принадлежит L1. Язык L2 называется NP-трудным, если любой язык из класса NP сводится к нему. Язык называют NP-полным, если он NP-труден и при этом сам лежит в классе NP. Таким образом, если будет найден алгоритм, решающий хоть одну NP-полную задачу за полиномиальное время, все NP-задачи будут лежать в классе P.
Равенство классов P и NP уже более 30 лет является открытой проблемой. Научное сообщество склоняется к отрицательному решению этого вопроса — в этом случае за полиномиальное время решать NP-полные задачи не удастся.
5. МЕТОД ВЕТВЕЙ И ГРАНИЦ
Существует метод решения задачи коммивояжера, который дает оптимальное решение. Этот метод называется методом ветвей и границ.
Основа этого, ныне широко распространенного метода состоит в построении нижних оценок решения, которые затем используются для отбраковки неконкурентоспособных вариантов.
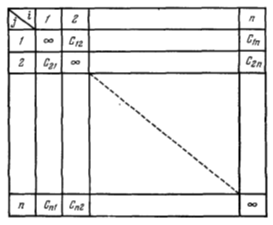
Функция f(xi, xj) принимает конечное число значений сij, которые мы можем представить в виде таблицы (Рисунок 5.1). Предположим, что мы выбрали некоторый путь Ss. Его длина будет равна
(5.1)
причем сумма (5.1) распространена по i, j так, что каждый из индексов встречается в ней один и только один раз. Величины сij с двумя одинаковыми индексами мы приняли равными ∞.
Так как в каждый из вариантов s входит только один элемент из каждой строки и столбца, то мы можем проделать следующую операцию, которая здесь называется приведением матрицы. Обозначим через hi наименьший элемент из строки номера i и построим новую матрицу С(1) с элементами
Матрица С(1) определяет новую задачу коммивояжера, которая, однако, в качестве оптимальной будет иметь ту же последовательность городов. Между величинами ls и ls(1) будет существовать, очевидно, следующая связь:
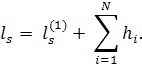
Заметим, что в каждой из строк матрицы С(1) будет теперь, по крайней мере, один нулевой элемент. Далее обозначим через gj наименьший элемент матрицы С(1), лежащий в столбце номера j, и построим новую матрицу С(2) с элементами
Величины hi и gj называются константами приведения. Оптимальная последовательность городов для задачи коммивояжера с матрицей С(2) будет, очевидно, такой же, как и для исходной задачи, а длины пути для варианта номера s в обоих задачах будут связаны между собой равенством
(5.2)
где
(5. 3)
т. Е. d0 равна сумме констант приведения.
Обозначим через l* решение задачи коммивояжера, т.е.
где минимум берется по всем вариантам s, удовлетворяющим условию (α) Тогда величина d0 будет простейшей нижней оценкой решения:
(5.4)
Будем рассматривать теперь задачу коммивояжера с матрицей С(2) которую мы будем называть приведенной матрицей.
Рассмотрим путь, содержащий непосредственный переход из города номера i в город номера j, тогда для пути s, содержащего этот переход, мы будем иметь, очевидно, следующую нижнюю оценку:
Следовательно, для тех переходов, для которых 
= 0, мы будем иметь снова оценку (5.4). Естественно ожидать, что
кратчайший путь содержит один из таких переходов — примем это соображение в
качестве рабочей гипотезы. Рассмотрим один из переходов, для которого 
=0, и обозначим через 
множество всех тех путей, которые не содержат перехода из i в j.
Так как из города i мы должны куда-то выйти, то
множество 
содержит один из переходов i→k, где k ≠ j; так как в город номера j мы должны прийти, то
множество 
содержит переход m→j, где т ≠ i.
Следовательно, некоторый путь ls из множества (ij), содержащий переходы i→k и m→j, будет иметь следующую нижнюю оценку:
Обозначим через
Тогда очевидно, что для
любого ls из множества путей 
мы будем иметь оценку
(5.5)
Мы предполагаем исключить некоторое множество вариантов 
,
поэтому мы заинтересованы выбрать такой переход i → j, для которого оценка (5.5) была бы самой высокой. Другими
словами, среди нулевых элементов матрицы С(2) выберем
тот, для которого 
максимально.
Это число обозначим через 
Таким
образом, все множество возможных вариантов мы разбили на два множества I1 и I2. Для путей из множества I1, мы имеем оценку (5.4). Для
путей из множества I2 оценка будет следующей:
(5.6)
Рассмотрим теперь множество I1 и матрицу С(2). Так как все пути, принадлежащие этому множеству, содержат переход i → j , то для его исследования нам достаточно рассмотреть задачу коммивояжера, в которой города номеров i и j совпадают. Размерность этой задачи будет уже равна N – 1, а ее матрица получится из матрицы С(2) вычеркиванием столбца номера j и строки но мера i.
Поскольку i → j невозможен, то элемент 
принимаем равным бесконечности.
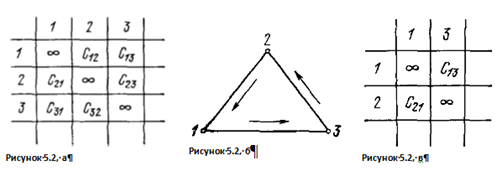
Рассмотрим случай N=3 (Рисунок 5.2, а), и предположим, что мы рассматриваем тот вариант, который содержит переход 3 → 2. Тогда задача коммивояжера после вычеркивания третьей строки и второго столбца вырождается в тривиальную. Ее матрица изображена на рисунке 5.2, в. В этом случае мы имеем единственный путь, и его длина будет, очевидно, равна сумме
Итак, если в результате вычеркивания строки номера i и столбца номера j мы получим матрицу второго порядка, то задачу можно считать решенной.
