Быстрый поиск

Курсовая работа: Транспортная задача линейного программирования

Транспортная задача с избытком запасов.

Сведем её к ранее рассмотренной транспортной задаче с правильным балансом. Для этого, сверх имеющихся n пунктов назначения В1, B2, ... , Bn, введём ещё один, фиктивный, пункт назначения Bn+1, которому припишем фиктивную заявку, равную избытку запасов над заявками

bn+1 = å аi - å bj ( где i=1,...,m ; j=1,...,n ) ,

а стоимость перевозок из всех пунктов отправления в фиктивный пункт назначения bn+1 будем считать равной нулю. Введением фиктивного пункта назначения B n+1 с его заявкой b n+1 мы сравняли баланс транспортной задачи, и теперь ее можно решать, как обычную транспортную задачу с правильным балансом.

Транспортная задача с избытком заявок.

Эту задачу можно свести к обычной транспортной задаче с правильным балансом, если ввести фиктивный пункт отправления Am+1 с запасом am+1 равным недостающему запасу, и стоимость перевозок из фиктивного пункта отправления во все пункты назначения принять равной нулю.

Задача, двойственная к транспортной.

Построим задачу, двойственную к транспортной. С этой целью вспомним, что каждому пункту отправления и назначения отвечает определенное ограничение

(6.1)

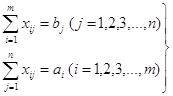
В то же время каждому ограничению из (6.1) сопоставляется определенная неизвестная в двойственной задаче. Тем самым устанавливается соответствие между всеми пунктами и и всеми неизвестными двойственной задачи.

Обозначим неизвестную в двойственной задаче, отвечающую пункту отправления , через , а пункту назначения – через .

Каждому неизвестному в транспортной задаче соответствует ограничение, связывающее неизвестные в двойственной задаче. Неизвестное входит ровно в два ограничения системы (6.1): одно из них отвечает пункту , а другое – пункту . В обоих этих уравнениях коэффициент при равен 1. Поэтому соответствующее ограничение в двойственной задаче имеет вид

(6.2)

Правая часть неравенства (6.2) равна , потому что именно с этим коэффициентом неизвестная входит в минимизируемую формулу (2.4).

Оптимизируемая форма двойственной задачи имеет вид

(6.3)

Таким образом, задача двойственная к транспортной формулируется следующим образом. При ограничениях (6.2) максимизировать формулу (6.3). Подчеркнем, что знак значений неизвестных и может быть произвольным.

Предположим, что нам известно некоторое допустимое базисное решение транспортной задачи, в котором все базисные неизвестные строго положительны. Это решение оптимально лишь в том случае, когда соответствующая ей система оказывается совместной. Эта система возникает из системы (6.2), если в ней все неравенства, отвечающие базисным неизвестным заменить точными равенствами.

В итоге приходим к соотношению:

(6.4)

(для всех свободных неизвестных )

Тем самым мы убеждаемся, что признак оптимальности в работе по методу потенциалов совпадает с необходимым и достаточным условием оптимальности.

7.Пример решения транспортной задачи.

В городе N имеется 4 склада Аi, на которых хранится ткань (в рулонах) и 5 магазинов Bj, занимающихся продажей ткани. Ниже, в таблице, приведены данные по количеству рулонов на каждом складе, запросы магазинов и стоимость перевозки одного рулона из Аi в Bj. Необходимо составить такой план перевозок, при котором запросы магазинов будут удовлетворены при минимальной суммарной стоимости перевозок.

Магазины Склад	B1 (b1=40)	B2 (b2=50)	B3 (b3=15)	B4 (b4=75)	B5 (b5=40)
А1 (а1=50)	1,0	2,0	3,0	2,5	3,5
А2(а2=20)	0,4	3,0	1,0	2,0	3,0
А3(а3=75)	0,7	1,0	1,0	0,8	1,5
А4(а4=80)	1,2	2,0	2,0	1,5	2,5

В данном случае Σai=225 >Σbj=220 => имеем дело с открытой моделью транспортной задачи. Сведем ее к закрытой введением фиктивного магазина B6 с потребностью b5=225-220=5 и стоимостью перевозок сi6=0.Имеем таблицу:

Магазины Склад	B1 (b1=40)	B2 (b2=50)	B3 (b3=15)	B4 (b4=75)	B5 (b5=40)	B6 (b6=5)
А1 (а1=50)	1,0	2,0	3,0	2,5	3,5	0
А2(а2=20)	0,4	3,0	1,0	2,0	3,0	0
А3(а3=75)	0,7	1,0	1,0	0,8	1,5	0
А4(а4=80)	1,2	2,0	2,0	1,5	2,5	0