 Курсовая работа: Решение задачи коммивояжера методом ветвей и границ
Курсовая работа: Решение задачи коммивояжера методом ветвей и границ
10) Находим константу приведения для множества контуров
![]() :
:![]()
Следовательно, нижняя
граница множества ![]() равна
равна
![]()
11) Сравниваем нижние
границы подмножеств ![]() и
и ![]() . Так как
. Так как
![]()
то дальнейшему ветвлению
подвергаем множество ![]() .
.
На рис.1 представлено ветвление по дуге (1;5).
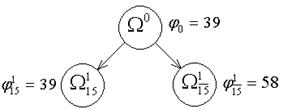
Рис.1
Переходим к ветвлению
подмножества ![]() . Его приведенная матрица
представлена в таблице ниже.
. Его приведенная матрица
представлена в таблице ниже.
|
j i |
1 | 2 | 3 | 4 | 6 |
| 2 |
03 |
∞ | 8 |
02 |
8 |
| 3 | 22 |
04 |
∞ | 26 | 4 |
| 4 | 3 |
00 |
17 | ∞ |
04 |
| 5 | ∞ |
010 |
17 | 10 | 47 |
| 6 | 37 | 12 |
010 |
2 | ∞ |
12) Узнаем степени нулей
матрицы. Претендентами на включение в гамильтонов контур будут несколько дуг
(5;2) и (6;3). Для дальнейших расчетов выберем дугу (6;3). Разбиваем множество ![]() на два
подмножества:
на два
подмножества:![]() и
и ![]() (табл. 3 и 4). Чтобы не допустить
образования негамильтонова контура, в таблице 3 заменяем элемент (3;6) на знак
«∞»
(табл. 3 и 4). Чтобы не допустить
образования негамильтонова контура, в таблице 3 заменяем элемент (3;6) на знак
«∞»
Табл.3
|
j i |
1 | 2 | 4 | 6 |
| 2 | 0 | ∞ | 0 | 8 |
| 3 | 22 | 0 | 26 | ∞ |
| 4 | 3 | 0 | ∞ | 0 |
| 5 | ∞ | 0 | 10 | 47 |
Табл.4
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9


