 Курсовая работа: Разбиение Делоне
Курсовая работа: Разбиение Делоне
![]() . 1 0 0 0
. 1 0 0 0
![]() ; 1 2 0 0
; 1 2 0 0
![]() ; 2 4 0 0
; 2 4 0 0
![]() ; 2 4 0 0
; 2 4 0 0
![]() ; 1 2 0 0
; 1 2 0 0
![]() ; 1 2 0 0
; 1 2 0 0
![]() ; 1 2 0 0
; 1 2 0 0
![]() ; 1 2 0 0
; 1 2 0 0
![]() ;
; ![]() 2 3 0 1
2 3 0 1
![]() ; 1 2 0 0
; 1 2 0 0
![]() ; 1 2 0 0
; 1 2 0 0
![]() ,
, ![]() ; 1 2 0 1
; 1 2 0 1
![]() ,
, ![]() ; 1 1 1 1
; 1 1 1 1
![]() 1 0 0 0
1 0 0 0
![]() ; 2 2 0 0
; 2 2 0 0
![]() . 2 2 0 0
. 2 2 0 0
26 32 1 3
+ * ![]() if
if
5 Описание работы программы
Создаем в оболочке WPF три круга которые можно передвигать при помощи нажатия левой кнопки мыши с1, с2, с3. И два круга которые будут прорисовываться в результате вычисления формул с4 и с5.
<Window x:Class="DeloneCircleWPF.MainWindow"
xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
Title="MainWindow" Height="350" Width="525" KeyDown="Window_KeyDown" xmlns:chartingToolkit="clr-namespace:System.Windows.Controls.DataVisualization.Charting;assembly=System.Windows.Controls.DataVisualization.Toolkit" MouseWheel="Window_MouseWheel">
<Canvas>
<Ellipse Name="c1" Width="100" Height="100" Canvas.Left="100" Canvas.Top="100" Fill="#E0FF0000" MouseLeftButtonDown="Ellipse_MouseLeftButtonDown" MouseLeftButtonUp="Ellipse_MouseLeftButtonUp" MouseMove="Ellipse_MouseMove"/>
<Ellipse Name="c2" Width="100" Height="100" Canvas.Left="200" Canvas.Top="100" Fill="#E000FF00" MouseLeftButtonDown="Ellipse_MouseLeftButtonDown" MouseLeftButtonUp="Ellipse_MouseLeftButtonUp" MouseMove="Ellipse_MouseMove"/>
<Ellipse Name="c3" Width="100" Height="100" Canvas.Left="150" Canvas.Top="200" Fill="#E00000FF" MouseLeftButtonDown="Ellipse_MouseLeftButtonDown" MouseLeftButtonUp="Ellipse_MouseLeftButtonUp" MouseMove="Ellipse_MouseMove"/>
<Ellipse Name="c4" Width="0" Height="0" Canvas.Left="0" Canvas.Top="0" Fill="Black"
Stroke="Black"/>
<Ellipse Name="c5" Width="0" Height="0" Canvas.Left="0" Canvas.Top="0" Stroke="Silver"/>
</Canvas>
</Window>
Создаем переменные для начальных координат Х и У, для события если мышь нажата, и для выгибания круга.
double beginX = 0;
double beginY = 0;
bool isMouseDown = false;
Shape shape;
Несколько функций для подкрепления рисунка с работой мыши.
private void Ellipse_MouseLeftButtonDown(object sender, MouseButtonEventArgs e)
{
shape = (Shape)sender;
Ellipse b = sender as Ellipse;
beginX = e.GetPosition(this).X;
beginY = e.GetPosition(this).Y;
isMouseDown = true;
b.Opacity = 0.5;
b.SetValue(Canvas.ZIndexProperty, 1);
b.CaptureMouse();
}
private void Ellipse_MouseLeftButtonUp(object sender, MouseButtonEventArgs e)
{
Ellipse b = sender as Ellipse;
isMouseDown = false;
b.Opacity = 1.0;
b.SetValue(Canvas.ZIndexProperty, 0);
b.ReleaseMouseCapture();
}
private void Ellipse_MouseMove(object sender, MouseEventArgs e)
{
if (isMouseDown)
{
Ellipse b = sender as Ellipse;
double currX = e.GetPosition(this).X;
double currY = e.GetPosition(this).Y;
double left = (double)b.GetValue(Canvas.LeftProperty);
double top = (double)b.GetValue(Canvas.TopProperty);
b.SetValue(Canvas.LeftProperty, left + currX - beginX);
b.SetValue(Canvas.TopProperty, top + currY - beginY);
beginX = currX;
beginY = currY;
ReCalclateDeloneCircle();
}
}
private void Window_KeyDown(object sender, KeyEventArgs e)
{
switch (e.Key)
{
case Key.Left:
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) - 1);
break;
case Key.Right:
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) + 1);
break;
case Key.Up:
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) - 1);
break;
case Key.Down:
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) + 1);
break;
case Key.PageUp:
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) - 1);
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) - 1);
shape.Width += 2;
shape.Height += 2;
break;
case Key.PageDown:
if (shape.Width - 2 >= 0)
{
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) + 1);
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) + 1);
shape.Width -= 2;
shape.Height -= 2;
}
break;
case Key.Tab:
if (shape == c1)
shape = c2;
else
if (shape == c2)
shape = c3;
else
shape = c1;
break;
case Key.Escape:
Close();
break;
}
ReCalclateDeloneCircle();
}
private void Window_MouseWheel(object sender, MouseWheelEventArgs e)
{
int k = Math.Abs(e.Delta) / e.Delta;
if (shape.Width + 2 * k >= 0)
{
shape.SetValue(Canvas.LeftProperty, (double)shape.GetValue(Canvas.LeftProperty) - k);
shape.SetValue(Canvas.TopProperty, (double)shape.GetValue(Canvas.TopProperty) - k);
shape.Width += 2 * k;
shape.Height += 2 * k;
}
ReCalclateDeloneCircle();
}
Функции для определения радиусов кругов Делоне, и для переопределения по мере передвижения кругов по рабочему окну.
private void ReCalclateDeloneCircle()
{
double r1 = c1.Width / 2;
double x1 = (double)c1.GetValue(Canvas.LeftProperty) + r1;
double y1 = (double)c1.GetValue(Canvas.TopProperty) + r1;
double r2 = c2.Width / 2;
double x2 = (double)c2.GetValue(Canvas.LeftProperty) + r2;
double y2 = (double)c2.GetValue(Canvas.TopProperty) + r2;
double r3 = c3.Width / 2;
double x3 = (double)c3.GetValue(Canvas.LeftProperty) + r3;
double y3 = (double)c3.GetValue(Canvas.TopProperty) + r3;
double x4, y4, r4, x5, y5, r5;
CalclateDeloneCircle(x1, y1, r1, x2, y2, r2, x3, y3, r3, out x4, out y4, out r4, out x5, out y5, out r5);
r4 = Math.Abs(r4);
if (!double.IsInfinity(r4))
{
c4.SetValue(Canvas.LeftProperty, x4 - r4);
c4.SetValue(Canvas.TopProperty, y4 - r4);
c4.Width = 2 * r4;
c4.Height = 2 * r4;
}
r5 = Math.Abs(r5);
if (!double.IsInfinity(r4))
{
c5.SetValue(Canvas.LeftProperty, x5 - r5);
c5.SetValue(Canvas.TopProperty, y5 - r5);
c5.Width = 2 * r5;
c5.Height = 2 * r5;
}
}
private void CalclateDeloneCircle(
double x1, double y1, double r1,
double x2, double y2, double r2,
double x3, double y3, double r3,
out double x4, out double y4, out double r4,
out double x5, out double y5, out double r5)
{
double x21 = x2 - x1;
double y21 = y2 - y1;
double r21 = r2 - r1;
double x31 = x3 - x1;
double y31 = y3 - y1;
double r31 = r3 - r1;
double XY = x21 * y31 - x31 * y21;
if (XY == 0)
{
x4 = double.NaN;
y4 = double.NaN;
r4 = double.NaN;
x5 = double.NaN;
y5 = double.NaN;
r5 = double.NaN;
return;
}
double z21 = (x21 * x21 + y21 * y21 - r21 * r21) / 2;
double z31 = (x31 * x31 + y31 * y31 - r31 * r31) / 2;
double Ax = y21 * r31 - y31 * r21;
double Ay = -(x21 * r31 - x31 * r21);
double Bx = -(y21 * z31 - y31 * z21);
double By = x21 * z31 - x31 * z21;
double A = Ax * Ax + Ay * Ay - XY * XY;
double B = Ax * Bx + Ay * By;
double C = Bx * Bx + By * By;
double D = B * B - A * C;
if (D < 0)
{
x4 = double.NaN;
y4 = double.NaN;
r4 = double.NaN;
x5 = double.NaN;
y5 = double.NaN;
r5 = double.NaN;
return;
}
double R;
R = (-B - Math.Sqrt(D)) / A;
r4 = R - r1;
y4 = (Ay * R + By) / XY + y1;
x4 = (Ax * R + Bx) / XY + x1;
R = (-B + Math.Sqrt(D)) / A;
r5 = R - r1;
y5 = (Ay * R + By) / XY + y1;
x5 = (Ax * R + Bx) / XY + x1;
}
6. Вид рабочего приложения
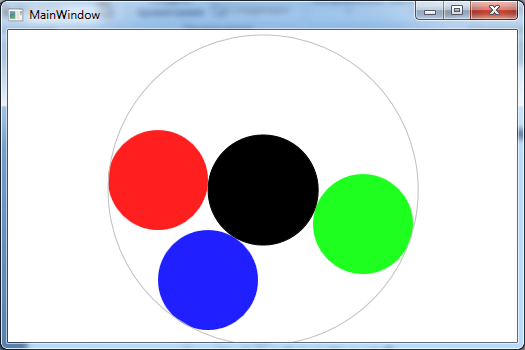
Рис. 6.1
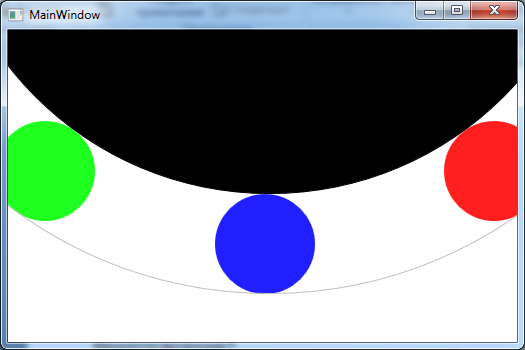
Раис 6.2
ВЫВОДЫ
Данная программа демонстрирует возможности программирования с помощью технологии Microsoft Windows Presentation Foundation. В этой программе наглядно показано новшества, которые WPF внесло в программирование Windows приложений, а именно: новое визуальное оформление, новая философия настройки элементов, новые графические средства и новый программный интерфейс.WPF состоит из двух взаимосвязанных программных интерфейсов. Программы WPF могут быть полностью написаны на C# или любом другом языке программирования, компилируемом в соответствии с правилами .NET CLS(Common Language Specification). Кроме того, WPF содержит новый язык разметки на базе XML, называемый XAML( eXtensible Application Markup Language).В отдельных случая на XAML можно написать целую программу, однако это приложение построено как из программного кода, так и из кода разметки. В этой программе XAML используется для определения пользовательского интерфейса, а программный код – для обработки событий. Подводя итоги можно сказать, что данная программа показывает преимущества технологии WPF над технологией Windows Forms.
Список литературы
1. Медведев Н.Н. Метод Вороного – Делоне в исследовании структуры некристаллических систем / РАН, Сиб. отд-ние, РФФИ, Институт химической кинетики и горения СО РАН. Новосибирск: НИЦ ОИГГМ СО РАН, Издательство СО РАН, 2000, 214 с.


