 Курсовая работа: Разбиение Делоне
Курсовая работа: Разбиение Делоне
Курсовая работа: Разбиение Делоне
ВведениеВ последние годы, в связи с применением многогранников Вороного и симплексов Делоне в самых различных науках, появляется интерес к истории возникновения этих геометрических построений. В ходе нашей работы мы рассмотрим математическую сторону метода Делоне, обсудим идеи и основные результаты. Как известно, Борис Николаевич был одним из учеников известного математика Г.Ф. Вороного. И поэтому результаты работ Делоне очень тесно связаны с методами Вороного.
Существует довольно много областей наук, где используются методы этих двух замечательных математиков. Кроме физики, математики и химии можно отметить наиболее известные: астрономию (изучение структуры Вселенной), экономику (методы оптимизации), картографию, экологию и компьютерную графику. Но все же главным полем применения методов в наше время являются математические науки.
Следует рассказать об одной простой, но важной теории, которую Борис Николаевич начал еще в начале 1920-х годов, — о так называемом методе пустого шара и связанном с ним разбиении пространства на специальные многогранники. Где-то в 1980-е годы, уже после смерти Б. Н. Делоне, эти разбиения получили название «триангуляции Делоне».
В нашей работе мы исследовали один из его методов – построение круга Делоне для трех многоугольников, а также вычисление радиуса и центра круга.
Раздел 1 Основные результаты работ Делоне
Борис Николаевич Делоне прожил долгую и плодотворную жизнь, внеся свой вклад в теорию чисел, алгебру и геометрию, а также воспитав многих выдающихся учеников. Делоне был чрезвычайно одаренным человеком, неутомимым альпинистом, талантливым педагогом. Заслуга Делоне еще в том, что он мог изложить фундаментальные математические результаты, как свои, так и других авторов, простым и наглядным языком, понятным не только математикам.
Работы Делоне тесно связаны с результатами работ Вороного. Классические результаты Вороного и Делоне получены для систем точек (центров). Объектом нашего исследования является система точек, произвольно расположенных в пространстве. Наши точки обособлены одна от другой, и в системе точек нет бесконечно больших пустот. Делоне сформулировал это следующим образом:
a) Можно указать некоторый конечный радиус (пусть даже очень маленький), такой, что внутри сферы этого радиуса, построенной вокруг любой точки системы, нет других точек, принадлежащих данной системе.
b) Можно указать другой конечный радиус (пусть даже очень большой), такой, что внутри сферы этого радиуса, расположенной в любом месте нашей системы, всегда найдется хотя бы одна точка системы.
Никаких других ограничений нет. Точки могут располагаться как упорядоченно, так и случайно. Будем обозначать такую систему как {А}, поскольку наши точки обычно являются центрами атомов.
2 Разбиение Делоне
2.1 Метод пустого шара Делоне. Симплекс Делоне
Воспользуемся пустым шаром, который мы будем перемещать, изменяя его размер так, чтобы он мог касаться точек системы {А}, но всегда оставался пустым.
Итак, поместим в систему точек {А} пустой шар Делоне. Это всегда возможно, если выбрать шар достаточно малым. Начнем увеличивать его радиус, оставляя центр шара на месте. В какой-то момент поверхность шара встретит некоторую точку i системы {А}. Это обязательно произойдет, ибо в нашей системе нет неограниченно больших пустот. Будем продолжать увеличивать радиус пустого шара так, чтобы точка i оставалась на его поверхности. Для этого придется двигать центр шара от точки i. Рано или поздно шар достигнет своей поверхностью другой точки системы {А}.
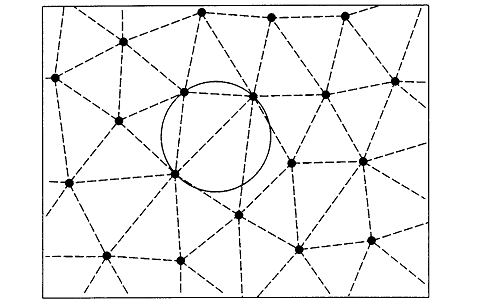
Рисунок 2.1 – Разбиение Делоне двумерной системы точек
Симплексы Делоне заполняют пространство без щелей и наложений.
Описанная сфера любого симплекса не содержит внутри себя других точек системы.
Пусть это будет точка j. Продолжим увеличивать радиус нашего шара, сохраняя уже обе точки на его поверхности. Увеличиваясь, шар достигнет какой-то третьей точки системы, точки k. В двумерном случае наш «пустой круг» в этот момент зафиксируется, т.е. станет невозможным дальнейшее увеличение его радиуса при сохранении круга пустым. При этом мы выявляем элементарную двумерную конфигурацию трех точек (i,j,k), определяющую некий треугольник, особенностью которого является то, что внутри его описанной окружности нет других точек системы {А}. В трехмерном пространстве шар не определяется тремя точками. Продолжим увеличивать его радиус, сохраняя все три найденные точки на его поверхности. Это будет возможно до тех пор, пока поверхность шара не встретится с четвертой точкой l системы. После этого движение и рост пустого шара станут невозможными. Найденные четыре точки (i,j,k,l) определяют вершины тетраэдра, который характерен тем, что внутри его описанной сферы нет других точек системы {А}. Такой тетраэдр называется симплексом Делоне.
Симплексом в математике называют простейшую фигуру в пространстве данной размерности: тетраэдр – в трехмерном пространстве; треугольник – в двумерном. Произвольная тройка (четверка) точек системы, не лежащих в одной плоскости, всегда определяет некий симплекс. Однако он будет симплексом Делоне только с том случае, если его описанная сфера пуста. Другими словами, симплексы Делоне определяются особым выбором троек (четверок) точек в системе {А}.
Мы построили один симплекс Делоне, однако, помещая пустой шар в различные места и повторяя ту же процедуру, можно определить и другие. Утверждается, что совокупность всех симплексов Делоне системы {А} заполняет пространство без наложений и щелей, т.е. реализует разбиение пространства, но на этот раз на тетраэдры. Это разбиение называется разбиением Делоне (рисунок 1).
2.2 Вырождение
Мы ограничились тем фактом, что ровно четыре точки в пространстве фиксируют пустой шар. В общем случае возможно, чтоб на его поверхности оказалось больше, чем четыре точки системы. Например, если имеется октаэдрическая конфигурация точек, то на поверхности вписанного шара будет лежать шесть точек – вершин октаэдра, а если кубическая, то восемь. Можно представить произвольную конфигурацию любого числа точек, лежащих на одной сфере. Все такие конфигурации, если они имеются в системе, будут выявляться с помощью пустого шара Делоне. Если мы наткнулись поверхностью шара сразу на несколько точек системы {А}, то при дальнейшем увеличении радиуса будем сохранять их всех на его поверхности. Рано или поздно мы упремся в последнюю точку (или точки), которая остановит движение нашего пустого шара.
Итак, если на поверхности
пустого шара оказалось более четырех точек, будем их рассматривать как вершины некоего
несимплициального многогранника. Будем называть такой многогранник несимплициальным
полиэдром Делоне. Любой несимплициальный полиэдр Делоне может быть разбит на симплексы
Делоне. Однако сделать это можно различными способами. В двумерном случае для многоугольника
с N вершинами может реализоваться ![]() (число сочетаний
из N по три) различных симплексов. Каждое конкретное разбиение содержит всегда N-2
симплекса. В трехмерном пространстве можно построить
(число сочетаний
из N по три) различных симплексов. Каждое конкретное разбиение содержит всегда N-2
симплекса. В трехмерном пространстве можно построить ![]() различных симплексов
(рисунок 2). Однако, в отличии от двумерного случая, здесь в разных конкретных разбиениях
может быть различное число симплексов.
различных симплексов
(рисунок 2). Однако, в отличии от двумерного случая, здесь в разных конкретных разбиениях
может быть различное число симплексов.
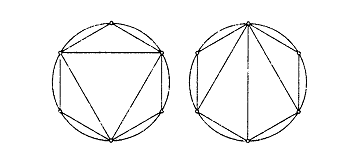
Рисунок 2 – Различные разложения двумерного несимплициального полиэдра на симплексы
Любой Х-угольник разбивается всегда на N-2 симплекса
Систему {A} будем называть вырожденной, если в ней имеется хотя бы один несимплициальный полиэдр Делоне, т.е. хотя бы один раз на поверхности пустого шара оказывается более четырех точек системы. Если нет ни одной такой конфигурации, то система называется невырожденной.
3 Теорема о разбиении Делоне
Теорема: Полиэдры Делоне системы {A} не входят друг в друга и заполняют все пространство, будучи смежными по целым граням. Разбиение пространства на полиэдры Делоне однозначно определяется системой {A} и, обратно, однозначно ее определяет.
Покажем, что полиэдры Делоне не входят друг в друга. Возьмем какие-либо два полиэдра Делоне системы {A}, обозначим их как D1 и D2, а описанные вокруг них сферы S1 и S2. Если S1 и S2 не пересекаются, то полиэдры D1 и D2 также не имеют общих точек и поэтому не входят друг в друга. Если же S1 и S2 пересекаются, то все вершины полиэдра D1 всегда лежат на той «шапочке» сферы S1, которая расположена вне сферы S2, поскольку по условию сфера S2 пуста (рисунок 3). Точно так же рассуждая, приходим к тому, что вершины полиэдра D2 лежат на той «шапочке» сферы S2, которая располагается вне сферы S1. Следовательно, вершины полиэдров D1 и D2 всегда лежат по разные стороны от хордальной плоскости этих сфер или, возможно, частично на ней самой. Это означает, что все точки полиэдров D1 и D2 должны лежать по разные стороны от этой плоскости, ибо все полиэдры Делоне – выпуклые многогранники. Отсюда следует, что никакие из них не входят друг в друга, но, возможно, касаются своими поверхностями.
Нужно убедиться, что полиэдры Делоне могут соприкасаться только по целым граням. Возьмем произвольную грань некоторого полиэдра D. Станем двигать центр описанной вокруг него сферы по направлению из полиэдра перпендикулярно этой грани.
разбиение симплекс делоне круг
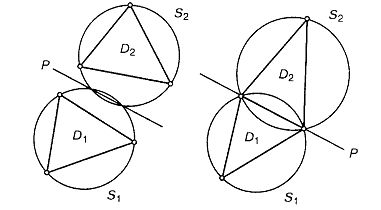
Рисунок 3 – К доказательству теоремы


