Курсовая работа: Нелинейные САУ
>
0
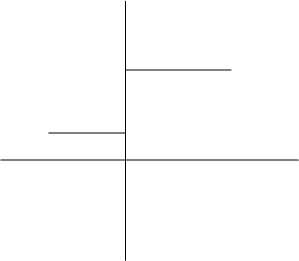
“а” “б”
 |
 |
“в” “г”
Рисунок 4.
В рассматриваемом случае (10) при
W
(p)=
, когда
W(p)= W
(p)G(p),
G(p)=
p+1,
годограф W(jw) системы на рис. 5.
j
W(jw)
w=¥
>
<
=
w=0
Рисунок 5.
В случае (10) справедливы графические формы на рис. 4 в,г, т.е. исследуемая система абсолютно устойчива в смысле кругового критерия (3) или (5) при
>
(14)
Интересно заметить, что достаточные условия абсолютной устойчивости по Ляпунову
а > 0 , y(t) > 0
и
a > c
для рассматриваемого случая совпадают с достаточными условиями абсолютной устойчивости, полученными для кругового критерия (14), если выполняется требование
y(t) > 0 (15)
поскольку, согласно (11) и (13) a=a
=
.
Докажем это, используя условия существования скользящего режима
-
k£y(t)=c
k
т.е. подставим сюда вместо коэфициентов а,с, и k их выражения через
,
, 
, тогда получим
-
£
y(t)=
£
(16)
Согласно рис. 5 и условия (16) получаем:
1) при 
= 
, y(t)=0
2) при 
> 
, y(t)>0
3) при 
< 
, y(t)<0,
что и требовалось доказать.
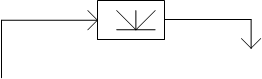
Теперь рассмотрим нашу систему с логическим алгоритмом управления, ее логическая схема приведена на рис. 6.
|x|=c
l g s
z
(-) x G(p) 
(p) 
Рисунок 6.
В данном случае считаем что:
-
варьируемая величина,
=0.5,
=0.1
(анализ поведения системы при изменении данного параметра исследуется в работе
ст-та Новикова, мы берем оптимальное значение),
=0.1,1
(коэффициент обратной связи),
=10,100.
Рассмотрим теперь саму функцию:
W(p)=G(p)W
(p),
где G(p) - функция корректора, W
(p)= 
(p)W
(p), где
(p)=
, а W
(p) в свою очередь будет:
