Курсовая работа: Нелинейные САУ

              (-)          

                        G(p)      g

                          Рисунок 2.

  Здесь W(p) - оператор линейной части системы, которая может иметь в общем случае следущий вид:

            W(p)=;                

                                               (8)

         W(p)=;

  Алгоритм регулятора имеет вид:

              y=Yx,

                               

              при gx>0          

      Y=                                     (9)

             - при gx<0,

        g=(

   В форме уравнений Коши рассматриваемая система имеет вид:

                               

         =,             

         =-,                  (10)

                                

  

                    k при g>0

       где    =

                   - k при g<0,        

             

          g=c+; =.

  Соответствие записей системы на рис. 2 достигается, когда при

W(p)= в уравнениях (10) имеем:

                          (11)  

а при W(p)=     имеем:

                         (12)

Причем для обоих случаев (11) и (12) имеет место соотношение

                                             (13)     

В соответствии с изложенным одинаково справедливо рассматривать в виде структурной схемы на рис. 2 с известным линейными операторами -  и G(p) или в виде формы Коши (10).

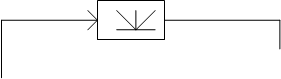
   Дополнительно отметим, что структурная интерпритация рассматриваемой системы на рис. 2 имеет еще одну структурную схему описания, приведенную на рис. 3.

                           |x|=c

 l                          g              y                z

 (-)    x         G(p)                           W(p)

                        Рисунок 3.

 

Это означает, что аналитической записи (10) соответствуют два структурных представления исследуемой СПС, причем второе позволяет рассматривать систему (10) как релейную систему с изменяемым ограничение, когда |x| - var.

   Далее перейдем к анализу нашего метода.

Согласно частотной теоремы (10), для абсолютной устойчивости системы на рис. 3 лостаточно, чтобы при всех w, изменяющихся от    - ¥ до + ¥, выполнялось соотношение:

            Re{[1+w)][1+W(jw)]}>0,

а гадограф mW(jw)+1 при  соответствовал критерию Найквиста.

  Для исследуемой системы условие (3) удобнее записать в виде

(4) и (5).

  На рис. 4 приведенны возможные нелинейные характеристики из класса М() и годографы W(jw), расположенные таким образом, что согласно (4) и (5) возможна абсолютная устойчивость.

           y ^

                 y=g   ()   

                   |x|        y=g (при =0)           

Страницы: 1, 2, 3, 4