Курсовая работа: Использование статистических функций в математическом пакете MathCAD

·  plnorm(x,m,s) - значение в точке x функции логарифмического нормального распределения;

·  plogis(x,l,s) - значение в точке x функции логистического распределения;

·  pnorm(x,m,s) - значение в точке x функции нормального распределения;

·  pnbinom(k,n,p) - значение в точке x функции отрицательного биномиального распределения;

·  ppois(k,l) - значение для k функции распределения Пуассона;

·  pt(x,d) - значение в точке x функции распределения Стьюдента;

·  punif(x,a,b) - значение в точке x функции равномерного распределения;

·  pweibull(x,s) - значение в точке x функции распределения Вейбулла.

6. Квантили распределения

Следующая группа задает обращения (квантили) функций распределения случайных величин. Они позволяют по заданной вероятности вычислить такое значение x, при котором вероятность равна или меньше заданного значения p:

·  qbeta(p,s1,s2) - квантили обратного бета-распределения с параметрами формы s1 и s2;

·  qbinom(p,n,q) - количество успешных определений при решении уравнения Бернулли, если число испытаний равно n, вероятность этого количества успешных определений равна p, а q - вероятность успеха при однократном испытании (0JqЈ1 и 0ЈpЈ1);

·  qcauchy(p,l,q) - квантили обратного распределения Коши со шкалой параметров l и s (s>0 и 0<p<1);

·  qchisq(p,d) - квантили обратного xи-квадрат-распределения;

·  qexp(p,r) - квантили обратного экспоненциального распределения, при котором параметр r>0 определяет частоту (0Јp<1);

·  qF(p,d1,d2) - квантили обратного распределения Фишера, в котором d1 и d2 - степени свободы;

·  qgamma(p,s) - квантили обратного гамма-распределения;

·  qgeom(p,q) - квантили обратного геометрического распределения;

·  qlnorm(p,m,s) - квантили обратного логарифмического нормального распределения;

·  qlogis(p,l,s) - квантили обратного логистического распределения;

·  qnbinom(p,n,q) - квантили обратного отрицательного биномиального распределения с размером n и вероятностью ошибки q;

·  qnorm(p,m,s) - квантили обратного нормального распределения со средним значением m и стандартным отклонением s;

·  qpois(p,l) - квантили обратного распределения Пуассона;

·  qt(p,d) - квантили обратного распределения Стьюдента (d определяет степени свободы, d>0 и 0 qunif(p,a,b) - квантили обратного равномерного распределения;

·  qweibull(p,s) - квантили обратного распределения Вейбулла.

7. Функции создания векторов с различными законами распределения

Последняя группа статистических функций служит для создания векторов с определенными законами распределения значений их элементов:

·  rbeta(m,s1,s2) - бета-распределение;

·  rbinom(m,n,p) - биномиальное распределение;

·  rcauchy(m,l,s) - распределение Коши;

·  rchisq(m,d) - хи-квадрат-распределение;

·  rexp(m,r) - экспоненциальное распределение,

·  rF(m,d1,d2) - распределение Фишера;

·  rgamma(m,s) - гамма-распределение;

·  rgeom(m,p) - геометрическое распределение;

·  rlnorm(m,m,s) - логарифмическое нормальное распределение;

·  rlogis(m,l,s) - логистическое распределение;

·  rnbinom(m,n,p) - отрицательное биномиальное распределение;

·  rnorm(m,m,s) - нормальное распределение;

·  rpois(m,l) - распределение Пуассона;

·  rt(m,d) - распределение Стьюдента;

·  runif(m,a,b) - равномерное распределение;

·  rweibull(m,s) - распределение Вейбулла.

На рис. 2. показан фрагмент документа MathCAD с примерами построения графиков различных статистических функций и задания наборов чисел с различным распределением.

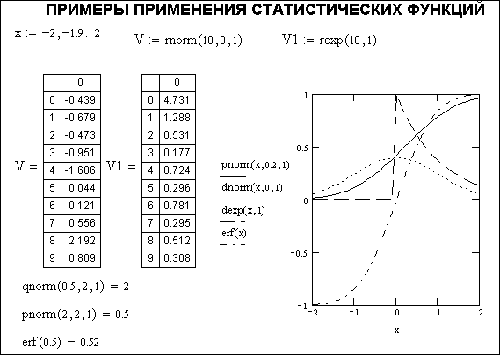
Рис. 2. Примеры применения статистических функций

Обилие статистических функций, включенных в систему MathCAD, позволяет с ее помощью выполнять достаточно сложные статистические расчеты. Однако все же надо отметить, что существуют более мощные специализированные пакеты для выполнения статистических расчетов, например Statistica или StatGraphics, которые заметно превосходят MathCAD в части многовариантности статистических вычислений.

1.  Линейная регрессия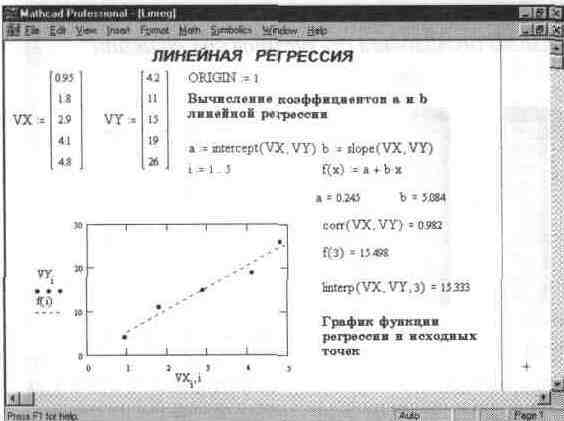

Рис.3. Линейная регрессия

Как видно на рис 3. прямая регрессии проходит в «облаке» исходных точек с максимальным среднеквадратичным приближением к ним. Чем ближе коэффициент корреляции к 1, тем точнее представленная исходными точками зависимость приближается к линейной.

2.  Функции для линейной регрессии

Другой широко распространенной задачей обработки данных является представление их совокупности некоторой функцией у(х). Задача регрессии заключается в получении параметров этой функции такими, чтобы функция приближала облако исходных точек (заданных векторами VX и VY) с наименьшей среднеквадратичной погрешностью. Чаще всего используется линейная регрессия, при которой функция у(х) имеет вид:

у(х) =а+ Ь*х

и описывает отрезок прямой. К линейной регрессии можно свести многие виды нелинейной регрессии при двухпараметрических зависимостях у(х).

Для проведения линейной регрессии в систему встроен ряд приведенных ниже функций:

·  corr(VX, VY) — возвращает скаляр — коэффициент корреляции Пирсона;

·  intercept(VX, VY) — возвращает значение параметра а (смещение линии регрессии по вертикали);

·  slope(VX, VY) — возвращает значение параметра b (наклона линии регрессии).

3.  Линейная регрессия общего вида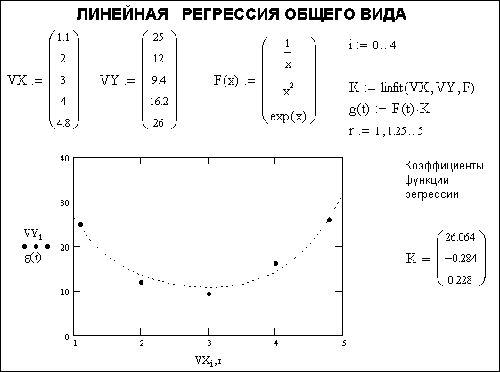

Рис. 4. Линейная регрессия общего вида

Расположение координат точек исходного массива может быть любым, но вектор VX должен содержать координаты, упорядоченные в порядке их возрастания, а вектор VY ординаты, соответствующие абсциссам в векторе VX.

8. Функция для линейной регрессии общего вида

В MathCAD реализована возможность выполнения линейной регрессии общего вида. При ней заданная совокупность точек приближается функцией вида:

F(x, К1 ,К2, ., Kn)= K1, F1(x)+K2 F2(x)+ +КnFn(x)

Таким образом, функция регрессии является линейной комбинацией функций F1(x), F2(x), ..., Fn(x), причем сами эти функции могут быть нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции.

Для реализации линейной регрессии общего вида используется функция linfit(VX,VY,F) Эта функция возвращает вектор коэффициентов линейной регрессии общего вида К, при котором среднеквадратичная погрешность приближения облака исходных точек, если их координаты хранятся в векторах VX и VY, оказывается минимальной Вектор F должен содержать функции F1(x), F2(x), , Fn(x), записанные в символьном виде.

9.
Полиномиальная регрессия

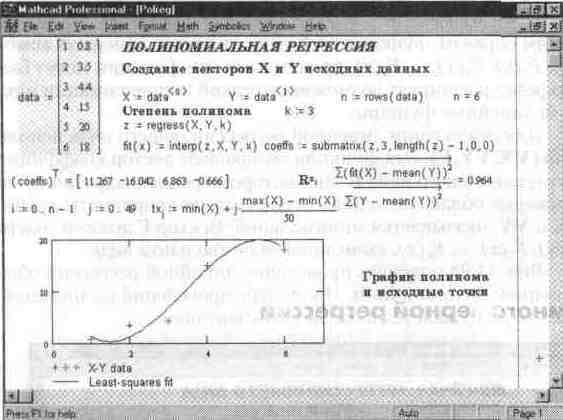
Рис. 5. Полиномиальная регрессия

На практике не рекомендуется делать степень аппроксимирующего поли нома выше четвертой — шестой, поскольку погрешности реализации регрессии сильно возрастают.

Функция regress создает единственный приближающий полином, коэффициенты которого вычисляются по всей совокупности заданных точек, т е глобально. Иногда полезна другая функция полиномиальной регрессии, дающая локальные приближения отрезками полиномов второй степени, — loess(VX, VY, span). Эта функция возвращает используемый функцией interp(VS,VX,VY,x) вектор VS, дающий наилучшее приближение данных (с координатами точек в векторах VX и VY) отрезками полиномов второй степени Аргумент span>0 указывает размер локальной области приближаемых данных (рекомендуемое начальное значение — 0,75).

 Чем больше span, тем сильнее сказывается сглаживание данных. При больших span эта функция приближается к regress(VX,VY,2).

На рис. 5. показан пример приближения сложной функции со случайным разбросом ее ординат с помощью совокупности отрезков полиномов второй степени (функция loess) для двух значений параметра span.

На рис. 5. нетрудно заметить, что при малом значении span, равном 0 05, отслеживаются характерные случайные колебания значений функции, тогда как уже при span=0,5 кривая регрессии становится практически гладкой. К сожалению, из-за отсутствия простого описания аппроксимирующей.

10. Функции для одномерной и многомерной полиномиальной регрессии

Введена в новую версию MathCAD и функция для обеспечения полиномиальной регрессии при произвольной степени полинома регрессии

regress(VX,VY, n)

Она возвращает вектор VS, запрашиваемый функцией interp(VS,VX,VY,x), содержащий коэффициенты многочлена п-й степени, который наилучшим образом приближает «облако» точек с координатами, хранящимися в векторах VX и VY.

11. Практическая часть

 

Тема: Использование статистических функции в математическом пакете MathCAD.

Цель: Создать регрессию.

Программные средства: математический пакет MathCAD.

Ход работы:

1.  Задаю вектора экспериментальных значений x и y.

2.  Присваиваю значение к переменной z и ввожу функцию regress(x, y, n)

3.  Вывожу результат переменной z

4.  Создаю график, задаю нужные значения

5.  Результат

Заключение

статистический функция регрессия распределение

В ходе работы были сделаны следующие выводы:

- автор узнал, что такое MathCAD, для чего он используется и узнал какие статистические функции бывают в MathCAD.

- так же автор узнал, по предложенным картинкам как выглядят те или иные функции.

Самооценка: автор считает, что он достиг поставленной цели и понятно изложил всю тему.

Значимость моей работы заключается в том что, я решил эту проблему, и теперь могу без проблем работать в MathCAD. Так же я узнал новое из этой работы, и те учащиеся, которые заинтересованы в этой теме тоже узнали нового. Конечно, возникла трудность с поиском литературы, материала для данной работы существует не так много.

Гипотеза автора подтвердилась, автор узнал, какие бывают статистические функции, и теперь он без проблем может работать в MathCAD.

Цель была достигнута, автор выяснил, какие бывают статистические функции.

Задачи этой работы были решены, автор узнал, что такое MathCAD и узнал какие бывают статистические функции/

Список литературы

1.  http://www.sistemair.ru/dok/mathcad12/Glava_12/Index03.htm

2.  http://www.piter.com/attachment.php?barcode=978531800362&at=exc&n=0

3.  http://ru.wikipedia.org/wiki/MathCad