Быстрый поиск

Курсовая работа: Градиентный метод первого порядка

Предложенный план эксперимента обладает следующими свойствами:

Свойство симметричности.

;

Свойство нормировки.

;

Свойство ортогональности.

, ( lj , l,i = 1…k );

Следует отметить, что ортогональные планы полный факторный эксперимент ( для линейных моделей ) обладают также рототабельностью. Последнее предполагает равенство и минимальность дисперсий предсказанных значений выходной переменной для всех точек факторного пространства. По закону накопления ошибок для дисперсии предсказанных уравнением регрессии значений выходной переменной можно записать:

s2y= s2b0 + s2b1U12 + … + s2bnUn2

Дисперсии коэффициентов регрессии равны между собою, поэтому

s2y = s2bi

С учетом того, что

Где - радиус сферы имеем

s2y = s2 bi.

Отсюда ясно, что дисперсия предсказанного значения выходной переменной зависит только от радиуса сферы. Это свойство рототабельности эквивалентно независимости дисперсии выходной переменной от вращения координат в центре плана и оправдано при поиске оптимума градиентными методами. Интуитивно понятно, что исследователю удобно иметь дело с такой информацией, содержащейся в уравнении регрессии, которая равномерно «размазана» по сфере радиусом . Действительно такое положение можно признать разумным, ибо с помощью уравнения регрессии будут предприниматься попытки предсказать положение ещё неизвестных участков факторного пространства. Равноценность этих участков в смысле ошибки предсказания, по-видимому, является необходимой.

Свойство ортогональности существенно облегчает процесс вычисления коэффициентов, так как корреляционная матрица (UТU)-1 становится диагональной, и коэффициенты будут равны 1/N;

6. С учетом свойства ортогональности можно вычислить вектор В коэффициентов регрессии:

Следовательно, любой коэффициент уравнения регрессии bj определяется скалярным произведением столбца Y на соответствующий столбец Uj, деленным на число опытов N в матрице планирования:

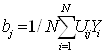
Вычислим коэффициенты регрессии линейного уравнения :

Если в рассмотрение ввести более полное уравнение регрессии с коэффициентами взаимодействия Р, то используя процедуру метода наименьших квадратов , получим:

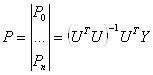Пользуясь планом, представленным в табл. 1.2, можно перечислить коэффициенты регрессии и записать в табл.1.4:

Y = Р0 + Р1U1 + Р2U2 + … + РnUn + … +

+…+ P13U1U3 + P23U2U3 + … + P123U1U2U3…

Таблица 1.4

Номер опыта	U0	U1	U2	…	Un	…				…	У
1	+1	+1	+1	…	+1	…	-1	+1	+1	…	У1
2	+1	-1	+1	…	+1	…	-1	-1	+1	…	У2
…	…	…	…	…	…	…	…	…	…	…	…
N	+1	-1	-1	…	-1	…	-1	+1	+1	…	УN