Контрольная работа: Обусловленность матрицы

Отсюда видим, что

Строим гистограмму элементов вектора относительных погрешностей d. (см. файл «Вектор и гистограмма»)

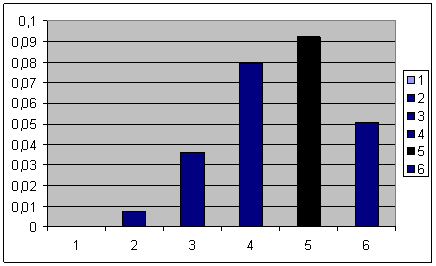
По гистограмме видно, что наибольшее влияние на погрешность решения оказывает компонента  вектора .

Найдем число обусловленности  матрицы A

Число обусловленности   матрицы A вычисляется по формуле

Норма матрицы A:      =57,3638

Норма обратной матрицы :      =129841,19

7448184,055

Теоретическая оценка погрешности

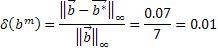
Так как   то матрица плохо обусловлена, это значит, что незначительные изменения в правой части приведут к большой погрешности в решении.

Задача 2 Метод хорд

Методом хорд найти корень уравнения  с точностью .

Решение

Найдем интервал, в котором находится корень:

Корнем уравнения является точка пересечения этих функций

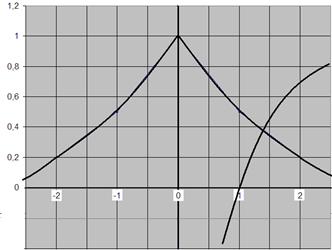
Из графика видно, что корень лежит в интервале .

Найдем неподвижный конец:

Для определения используем  horda.xls(см. приложение)

y(a)	-0,5	y(b)	0,493147		непод
y'(a)	1,5	y'(b)	0,66		1
y''(a)	-1,75	y''(b)	-0,426

Неподвижный конец -1

Выполняем приближение, используя horda.xls

Х	х0
1	2
xi	F(xi)	sigma
1,50345005	0,1010481	else
1,41881012	0,0179259	else
1,40431471	0,0030870	else
1,40183381	0,0005288	else
1,40140927	0,0000905	else
1,40133662	0,0000155	else
1,40132419	0,0000027	and

Окончание процесса – при  ,это и есть наш корень.

Задача 3 Решение СЛАУ

Решить систему уравнений ax=b, где

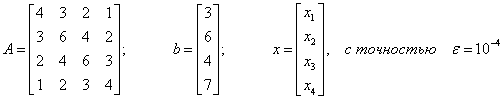
Вычислить точностные оценки методов по координатам: , - координаты численного решения,  - координаты точного решения.

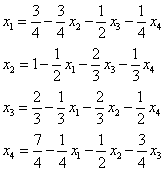
1.  Метод простых итераций

Сделаем расчет, используя SLAU.xls

х1	0,7500	-0,7500	-0,3333	-0,4375	-0,7708	0,7500
х2	1,0000	-0,3750	-0,4444	-0,5833	-0,4028	1,0000	1
х3	0,6667	-0,2500	-0,6667	-0,8750	-1,1250	0,6667
х4	1,7500	-0,1875	-0,5000	-0,5000	0,5625	1,7500

х1	0,7500	0,3021	0,5625	-0,1406	1,4740	-0,7708
х2	1,0000	0,3854	0,7500	-0,1875	1,9479	-0,4028	2
х3	0,6667	0,2569	0,2685	-0,2813	0,9109	-1,1250
х4	1,7500	0,1927	0,2014	0,8438	2,9879	0,5625

х1	0,7500	-1,4609	-0,4555	-0,7470	-1,9134	1,4740
х2	1,0000	-0,7370	-0,6073	-0,9960	-1,3402	1,9479	3
х3	0,6667	-0,4913	-1,2986	-1,4940	-2,6172	0,9109
х4	1,7500	-0,3685	-0,9740	-0,6832	-0,2756	2,9879

х1	0,7500	1,0052	1,3086	0,0689	3,1327	-1,9134
х2	1,0000	0,9567	1,7448	0,0919	3,7934	-1,3402	4
х3	0,6667	0,6378	0,8935	0,1378	2,3357	-2,6172
х4	1,7500	0,4784	0,6701	1,9629	4,8614	-0,2756

Решение, наиболее  близкое к точному, получено из таблицы 3

Страницы: 1, 2, 3, 4, 5, 6, 7, 8