Контрольная работа: Методы теории надёжности
Заполнение таблицы :
Первые два столбца заполняются на основании Таблицы № 2 из литературы «Надёжность устройств автоматики и телемеханики Учебное пособие и методические указания ». Вносим в исходные данные в строку Последняя цифра шифра № 8, в строку Число изделий до начала испытаний № 1600.
Третий столбец n(t) – число всех отказавших элементов за рассматриваемый промежуток времени, рассчитывается по формуле :
;
Например, за 1100 часов от начала работы число отказавших элементов составит: n(t) = n(1100) = n(100) + n(200) +n(300) + n(400) + n(500) + n(600) + n(700) + n(800) + n(900) + n(1000) + n(1100) = 53+48+43+40+36+33+28+25+24+24+23+22 = 399
Четвертый столбец Р(t) – вероятность безотказной работы системы
;
где: N0 – первоначальное число элементов, N0 =1600
Например: через 1100 часов после начала работы определим вероятность безотказной работы системы:
;
Пятый столбец Θ(t) – вероятность отказа, рассчитывается по формуле:
;
Для времени t=1100 часов
получаем: 
;
, если
провести округление до четвёртого знака после запятой получаем 
.
Шестой столбец : Nср- среднее число изделий, исправно работающих в данный промежуток времени, находим по формуле:
;
где: Ni – число элементов, исправно работающих в начале заданного интервала времени.
Ni+1 – число элементов, исправно работающих в конце заданного интервала времени.
Например: 
, 
, 
, 
, 
.
Седьмой столбец : λ(t) – интенсивность отказа, определяемая по формуле:
;
Например: 
, 
Восьмой столбец : a(t) – параметр потока отказов, определяемый по формуле:
;
где: N – первоначальное число элементов,
n(Δt) – число отказавших элементов в интервале времени Δt (100ч).
Например: n(Δt)=53; N=1600; Δt=100
;
n(Δt)=22; N=1600; Δt=100
.
Проверка:
;
Среднее время безотказной работы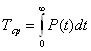 
. Статистическая оценка для
среднего времени наработки до отказа даётся формулой:
:
τi – наработка до первого отказа каждого из объектов.
где: N –число работоспособных объектов при t = 0;
Вывод: В процессе эксплуатации интенсивность отказов λ(t) снижалась и в конце установленного периода времени изменялась незначительно. Это говорит о том, что система приработалась и в данный момент находится в периоде нормальной эксплуатации. Система обладает достаточно высокой эксплуатационной надёжностью, среднее время безотказной работы составило 1298,9 ч,
Задача № 2 Расчёт количественных характеристик надёжности ИМС
Определить количественные характеристики надёжности Р(t), λ(t), a(t), Tср элементов системы (интегральных микросхем – ИМС), для времени их работы t = 500, 1000, 1500, 2000, 2500 часов, если время работы ИМС до отказа подчиняется закону распределения Релея. Данные о величине дисперсии σ выбираем из таблицы №4 литературы «Надёжность устройств автоматики и телемеханики Учебное пособие и методические указания ».В строку σ = вводим 1200 часов.
| P (t) | Θ(t) | λ (t) | a(t) | |
| 500 | 0.916855 | 0.083145 | 0.000347 | 0.000318 |
| 100 | 0.706648 | 0.293352 | 0.000694 | 0.000491 |
| 1500 | 0.457833 | 0.542167 | 0.001042 | 0.000477 |
| 2000 | 0.249352 | 0.0750648 | 0.001389 | 0.000346 |
| 2500 | 0.114162 | 0.885838 | 0.001736 | 0.000198 |
Первый столбец : t – время работы элементов системы;
