Дипломная работа: Спиральные антенны

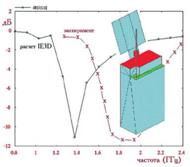
Рисунок 3.4.7. Частотная характеристика значительно отличается от экспериментально измеренной, поскольку программа IE3D не позволяет описывать трёхмерное диэлектрическое покрытие

Из анализа ДН видно, что крышка экранирует излучение штыря антенны. Она действует как экран на дальнее поле и значительно (на 4 дБ) уменьшает усиление в направлении за крышкой. Этот вывод подтверждается экспериментально.

Экспериментальные измерения диаграммы направленности в безэховой камере показали её сильное изменение по величине при открытой крышке. Методика измерения диаграммы направленности состоит в измерении чувствительности телефона на системном уровне (прибором, имитирующем базовую станцию). В данном случае регулируется общее усиление по петле усиления: передатчик базовой станции, передающая антенна, сотовый телефон, ориентированный в пространстве, и аппаратура приёмника базовой станции. При открытой крышке чувствительность некоторых телефонов падает до очень низкого уровня, и система не имеет возможности её измерить.

Глава 4. Расчёт диаграмма направленности плоских спиральных антенн

4.1 Типы нормальных волн и свойства симметрии спиральных антенн

Известные типы спиральных структур обладают либо симметрией вращения, либо винтовой симметрией, являющейся сочетанием симметрии вращения и трансляционной симметрии. Различные виды геометрической симметрии замедляющих систем и вытекающие из нее следствия относительно свойств электромагнитных полей. Воспользуемся основными известными общими положениями для рассмотрения электродинамических свойств спиральных структур. Напомним лишь, что симметрия вращения заключается в свойстве спирали совмещаться с собой при повороте вокруг некоторой оси на угол 2π/М, где М — целое число, равное числу заходов (плечей ) спирали. Эта симметрия характеризуется поворотной осью симметрии См.

При трансляционной симметрии спираль совмещается сама с собой при смещении ее вдоль оси на величину S/M, где S — шаг спирали. При винтовой симметрии спираль совмещается сама с собой при повороте вокруг оси на угол 2π/М и одновременном перемещении вдоль оси на S/M. Такая симметрия характеризуется винтовой осью симметрии Cм1. Точки структур, совмещающиеся при преобразованиях симметрии, называются симметричными.

Все известные типы спиралей имеют симметрию вращения, а винтовую симметрию – лишь цилиндрические бесконечные спирали с постоянным шагом S. Такие спирали ниже называются регулярными. Однозаходные плоские, конические и цилиндрические спирали имеют поворотную ось симметрии С1, двухзаходные — ось С2 и т. д. Регулярная однозаходная спираль имеет винтовую ось симметрии С11, двухзаходная—ось C21 и т. д.

Хотя конечная цилиндрическая спираль с постоянным шагом и не имеет трансляционной и винтовой симметрии, ее можно рассматривать как отрезок регулярной спирали с этими двумя видами симметрии, в котором существуют прямые и обратные волны. При анализе такой антенны можно использовать результаты, полученные для бесконечно длинной спирали.

В практических конструкциях спиральных антенн часто применяется диэлектрик в виде опорных цилиндров, на поверхность которых укладываются заходы. Если диэлектрик однороден в азимутальном и продольном направлениях, то свойства симметрии спиральной структуры не изменяются.

Для уменьшения поперечных размеров спиральной антенны можно использовать замедляющие системы, уменьшающие фазовую скорость тока в заходах спирали. Такая замедляющая система может быть однородной в азимутальном и продольном направлениях. Кроме того, проводник спирали может представлять собой замедляющую систему (например, спираль малого радиуса или зигзагообразную ленту), причем однородную вдоль спирального направления. В этих случаях свойства симметрии структуры также не изменяются. В дальнейшем предполагается, что и диэлектрик, и замедляющие системы не нарушают свойств симметрии.

Рассмотрим свойства полей в системах с различной симметрией.

Пусть рассматриваемая система имеет поворотную ось симметрии См, т.е. представляет собой М-заходную произвольную спираль — плоскую, коническую или цилиндрическую.

Как показано, поле произвольным образом возбужденной замедляющей системы с поворотной осью симметрии См можно представить в виде суммы М так называемых нормальных волн, каждая из которых удовлетворяет граничным условиям в системе. Вектор напряженности электрического поля в q-й нормальной волне может быть записан в виде

Eq (r, φ, z) =Е0q(r, φ, z)ехр[-ίqφ],(4.1.1)

где q- целое число, характеризующее тип волны,

-М/2<q≤Μ/2; Е0q — периодическая функция координаты φ цилиндрической системы координат, ось z которой совпадает с осью симметрии См. Период функции равен 2π/M и ее можно разложить в ряд Фурье:

Еоq(r,φ,z)=emq(r,z)exp[-imMφ] (4.1.2)

е — коэффициент разложения. Из (4.1.1) и (4.1.2) cледует выражение для поля q-й нормальной волны:

Eq(r,φ,z)=emq(r,z)exp[-ίνφ], (4.1.3)

где ν=qmΜ. (4.1.4)

Выражение (1.3) представляет собой разложение поля этой нормальной волны на так называемые азимутальные пространственные гармоники.

Аналогично можно представить токи в системе, соответствующие q-й нормальной волне:

jq(r,φ,z)=jmq(r,z) exp[-ίνφ]. (4.1.5)

Из (1.3) — (1.5) следует, что в q-ю нормальную волнy входят азимутальные пространственные гармоники с индексами ν=q+mM .

Поля и токи в соседних симметричных точках (в точках, совмещающихся при повороте системы вокруг оси| z на угол 2π/М) связаны соотношениями:

Еq (r, φ + 2π/М, z) = Еq (r,φ,z ) exp [-ί2πq/Μ]; (4.1.6)

jq (r,φ+2π/M, z) = jq (r,φ, z) exp [— ί2πq/M].

Из (4.2.6) следует, что поля и токи в указанных точках одинаковы по амплитуде и сдвинуты по фазе на 2πq/M. Если возбуждающие заходы спирали э. д. с. (или токи) одинаковы по амплитуде и сдвинуты по фазе на указанную величину, в системе возбуждается только q-я нормальная волна. В этой волне при заданных геометрических размерах спирали в зависимости от частоты может резонировать та или другая азимутальная пространственная гармоника, входящая в возбуждаемую нормальную волну. Резонирующая пространственная гармоника даст основной вклад в поле излучения и определяет диаграмму направленности, поляризационную и фазовую характеристики всей антенны в дальней зоне.

Аналогично поле произвольно возбужденной системы с винтовой осью симметрии СM1 также можно представить в виде суммы М нормальных волн, удовлетворяющих граничным условиям:

E(r, φ,z)=Eq (r,φ,z),

где для четных М

q1=1-Μ/2, q2= М/2,(4.1.7)

для нечетных М

q1=(1-M)/2, q2=(M-1)/2;

Eq(r, φ, z) = E0q(r, φ, z)ехр[-ί(β+ 2πq/S)z]. (4.1.8)

Функция E0q(r, φ, z) удовлетворяет условиям:

Е0q(r, φ, z)=E0q(r, φ, z + S/M), (4.1.9)

Е0q(r, φ+2π/Μ, z) = E0q(r, φ, z)exp[—ί2πq/M] (4.1.10)

и имеет периоды по z и φ соответственно S/M и 2π.

Разложив E0q(r, φ, z) в ряды Фурье по z и φ, получим

Е0q (r, φ, z)= et νq(r)exp[-ί2πΜtz/S]exp[-ίνφ] (4.1.11)

Из (1.10) и (1.11), приравнивая показатели экспонент, получаем следующее соотношение:

νφ+2πν/M=νφ+2πq/Μ+2πm, m=0, ±1, ±2, ..., (4.1.12)

отсюда ν=q+mM.

Из (4.1.8), (4.1.11) и (4.1.12) следует выражение для поля q-й нормальной волны:

Еq (r, φ, z)= 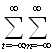enνq(r)exp[-ίβnz-ίνφ], (4.1.13)

βn=β+2πn/S, n=q+tM (4.1.14)

В аналогичном виде записывается выражение плотности тока проводимости, текущего в заходах спирали, соответствующего q-й нормальной волне:

jq(r, φ, z)=jn νq(r)exp[-ίβnz-ίνφ].

Выражение (4.1.13) представляет собой разложение вектора напряженности электрического поля q-й нормальной волны в ряд по азимутальным и так называемым продольным пространственным гармоникам, именуемым также φ- и z- гармониками .

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10