 Реферат: Cтатистика
Реферат: Cтатистика
К=-1 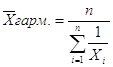
![]()
Пример Оценка 1-ый вопрос 2
2_ой вопрос 5
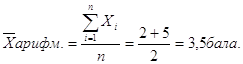
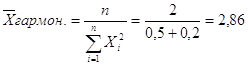
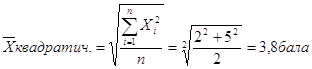
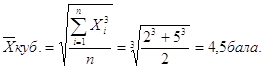
![]()
2,8<=3,05<=3,8<=4,05
13. Методы обоснования выбора формы средней величины. Структурные средние.
17. Понятие о моде, медиане
Структурные средние.
Для того чтобы определить среднее в некоторых случаях нет необходимости, или возможности прибегать к расчёту степенных средних в этих случаях появляется возможность или необходимость расчёта структурной средней .
Если величина средней (ср. арифметической) зависит от всех значений признака, встречаемых в данном распределении, то значение структурной средней определяется структурой распределения, местом распределения. Отсюда их названия.
Медиана – такое значение признака, которым обладает центральный член распределения ряда.
Вес телят
75 кг
80
83
87 (87+92)/2=89,5
92
97
101
пример
| Месяч. З/п (руб) --Х | Хi | Количество рабочих --f | Х*f | Накопленные частоты --S |
| До 800 | 700 | 1 | 700 | 1 |
| 800- 1000 | 900 | 2 | 1800 | 3 |
| 1000- 1200 | 1100 | 4 | 4400 | 7 |
| 1200- 1400 | 1300 | 1 | 1300 | 8 |
| 1400- более | 1500 | 2 | 3000 | 10 |
| Итого 10 | 11200 |
Медиана в интервальном ряду рассчитывается следующим образом.
Для определения медианы прежде всего исчисляют её порядковый
номер по формуле ![]() и строят ряд
накопленных частот . Накопленной частоте, которая равна порядковому номеру
медианы или первая его превышает, в дискретном вариационном ряду соответствует
вариант, являющийся медианой, а в интервальном вариационном ряду – медианный
вариант.
и строят ряд
накопленных частот . Накопленной частоте, которая равна порядковому номеру
медианы или первая его превышает, в дискретном вариационном ряду соответствует
вариант, являющийся медианой, а в интервальном вариационном ряду – медианный
вариант.
![]()
где Х0 – нижняя граница медианного интервала
d- величина медианного интервала
![]() --сумма частот или
весов рядов
--сумма частот или
весов рядов
Sме-1—сумма накопленных весов по интервалу предшествующему медианному
Fo-частота медианного интервала
Мода значение признака, которое чаще других встречается в данном ряду распределения.
Мода для дискретного ряда определяется как варианта, имеющая наибольшую частоту.
![]()
Где Хо –нижняя граница модального интервала.
d- величина интервала
f1- частота (вес) интервала, предшествующего модальному
f2—частота (вес) модального интервала.
F3—частота (вес) интервала, следующего за модальным.
Квартиль.
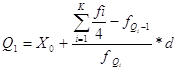
Q1-номер квартиля
![]() номер первого
квартильного значения признака
номер первого
квартильного значения признака
FQ1—частота квартильного интервала
FQ1-1 –сумма накопленных частот в интервале, предшествующего квартильному.
Q2=М
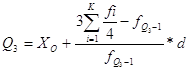
![]() -- номер
третьего квартильного признака
-- номер
третьего квартильного признака
Квартиль- структурное значение, которое отражает значение среднего признака в К-Л части.
Расчёт средних всегда производится одновременно с количественным анализом, изучаемых совокупностей, средние величины рассчитываются не всегда, когда на лицо количественная вариация признаков.
Формула для расчёта первого дециля.
![]()
Средняя величина должна быть рассчитываема для количественно-однородной совокупности.
Это требование состоит в том, что среднее нельзя применить к таким совокупностям, отдельные части которых подчинены различным законам развития относительных величин (определяемого)(усредняемого) признака.
14. Понятие вариации и значение ее статистического издания. Показатель вариации
Сущность и принципы вариации.
Абсолютные показатели вариации
Относительные показатели вариации.
Дисперсия альтернативного признака
Некоторые математические свойства дисперсии.
Исчисление среднего квадратического отклонения способом моментов.
Средняя величина представляет собой обобщающую статистическую характеристику в которой получает количественное выражение типичный уровень признака. Однако одной средней величиной нельзя отобразить все черты статистического распределения. При совпадении средних характер распределения может быть различен.
В связи с этим встаёт вопрос о расчёте показательной вариации.
Они используются для характеристики упорядочивания статистической совокупности.(Т.е. совокупности, которые подвергнуты группировкам, классификации и т.д.)
Для измерения вариации используются такие показатели, как размах вариации среднее линейное отклонение, дисперсия, средние квадратическое отклонение, каждый из этих показателей имеет свои познавательные возможности.
Простейший показатель –размах вариации.
R=Xmax-Xmin/
Из приведённой формы видно, что величина этого показателя целиком зависит от случайности расположения крайних членов ряда.
Его недостаток в том, что варьирование значения признака из основной массы членов ряда не находит отражения в этом показателе. В то же время колеблимость –признака складывается из всех его значений.
Таким образом применение такого показателя может привести к неправильной оценке вариации.
Указанного недостатка лишены такие показатели, которые представляют собой средние полученные из отклонений индивидуальных значений признака от их среднего размера.
![]()
![]()
L –может быть простой(выше) и взвешаной.
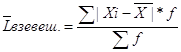
![]()
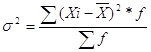
Среднее квадратическое отклонение
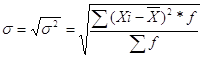
Для расчёта дисперсии в дискретном рядах используется следующая формула.
![]()
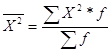
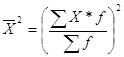
Пример Распределение коров колхозной фермы по годовому удою молока и расчёт абсолютных показателей вариации.
| Годовой удой молока от коровы тыс.кг. (Х) |
Число коров f |
Средняя величина признака Средина интервала |
Х*f | Х-Х | |X-X|*f | (X-X)2 | (X-X)2*f |
| До-2 | 4 | 1,5 | 6 | -1,3 | 5,2 | 1,69 | 6,76 |
| 2-3 | 2 | 2,5 | 5 | -ё,3 | 0,6 | 0,09 | 0,18 |
| 3-4 | 2 | 3,5 | 7 | +0,7 | 1,4 | 0,49 | 0,98 |
| 4-5 | 1 | 4,5 | 4,5 | +1,7 | 1,7 | 2,89 | 2,89 |
| 5 и более | 1 | 5,5 | 5,6 | +2,1 | 2,7 | 7,29 | 7,29 |
| Итого | 10 | 28 | 11,6 | 18,10 |
Находим среднюю арифметическую 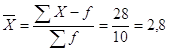
Страницы: 1, 2, 3, 4, 5, 6, 7, 8


