 Реферат: Общий обзор экспертных систем
Реферат: Общий обзор экспертных систем
Большинство ЭС включают знания, по содержанию которых их можно отнести одновременно к нескольким типам. Например, обучающая система может также обладать знаниями, позволяющими выполнять диагностику и планирование. Она определяет способности обучаемого по основным направлениям курса, а затем с учетом полученных данных составляет учебный план. Управляющая система может применяться для целей контроля, диагностики, прогнозирования и планирования. Система, обеспечивающая сохранность жилища, может следить за окружающей обстановкой, распознавать происходящие события (например, открылось окно), выдавать прогноз (вор-взломщик намеревается проникнуть в дом) и составлять план действий (вызвать полицию).
ГлаваII. Структура экспертной системы
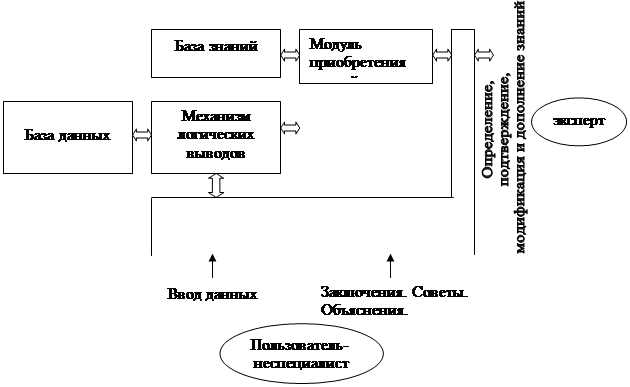
Структура экспертной системы представлена следующими структурными элементами:
1) База знаний – механизм представления знаний в конкретной предметной области и управления ими;
2) Механизм логических выводов – делает логические выводы на основании знаний, имеющихся в базе знаний;
3) Пользовательский интерфейс – используется для правильной передачи ответов пользователю;
4) Модуль приобретения знаний – служит для получения знаний от эксперта, поддержки базы знаний и дополнения ее при необходимости;
5) Модуль советов и объяснений – механизм, способный не только давать заключение, но и представлять различные комментарии, прилагаемые к этому заключению, и объяснять его мотивы. В противном случае пользователю будет трудно понять заключение. Такое понимание необходимо, если заключение используется для консультации или оказании помощи при решении каких-либо вопросов. Кроме того, с его помощью эксперт определяет, как работает система, и позволяет точно выяснить, как используются знания, предоставленные им.
Схема1
Структура экспертной системы
![]()
|
Пользовательский интерфейс
![]()
Глава III. Модели представления знаний
Одной из наиболее важных проблем, характерных для систем, основанных на знаниях, является проблема представления знаний. Это объясняется тем, что форма представления знаний оказывает существенное влияние на характеристики и свойства системы. Для того чтобы манипулировать всевозможными знаниями из реального мира с помощью компьютера, необходимо осуществлять их моделирование. В таких случаях необходимо отличать знания, предназначенные для обработки компьютером, от знаний, используемых человеком. Кроме того, при большом объеме знаний желательно упростить последовательное управление отдельными элементами знаний.
При проектировании модели представления знаний следует учитывать такие факторы, как однородность представления и простота понимания. Однородное представление приводит к упрощению механизма управления логическим выводом и упрощению управления знаниями. Представление знаний должно быть понятным экспертам и пользователям системы. В противном случае затрудняются приобретение знаний и их оценка. Однако выполнить это требование в равной степени, как для простых, так и для сложных задач довольно трудно. Обычно для несложных задач останавливаются на некотором среднем (компромиссном) представлении, но для решения сложных и больших задач необходимы структурирование и модульное представление.
Типичными моделями представления знаний являются:
1) Логическая модель;
2) Модель, основанная на использовании правил (продукционная модель);
3) Модель, основанная на использовании фреймов;
4) Модель семантической сети.
Однако во всех разработанных в прошлом системах с базами знаний помимо этих моделей использовались специальные для конкретного случая средства, поэтому представление знаний получалось сложным. Тем не менее классификация моделей оставалась неизменной. Язык, используемый для разработки систем, спроектированных на основе этих моделей, называется языком представления знаний.
3.1 Логическая модель представления знаний
Логическая модель используется для представления знаний в системе логики предикатов первого порядка и выведения заключений с помощью силлогизма. Основное преимущество использования логики предикатов для представления знаний заключается в том, что обладающий хорошо понятными математическими свойствами мощный механизм вывода может быть непосредственно запрограммирован. С помощью этих программ из известных ранее знаний могут быть получены новые знания.
Приведенные ниже примеры являются логическими моделями представления фактов с помощью предикатов и носят название атомарной формулы.
ЛЮБОВЬ (Виктор, Ирина): Виктор любит Ирину
СТОЛИЦА (Москва): Москва – столица
Следующие примеры являются правильно построенными логическими формулами,
включающими кванторы существования (![]() ) и
общности (
) и
общности (![]() ).
).
![]() : некий дельфин наделен
умственными способностями
: некий дельфин наделен
умственными способностями
![]() : все слоны имеют серую
окраску
: все слоны имеют серую
окраску
Отличительными чертами логических моделей, в частности приведенных выше моделей представления знаний, являются единственность теоретического обоснования и возможность реализации системы формально точных определений и выводов. По этим причинам немало исследователей в области искусственного интеллекта выбрали для себя предметом изучения именно логические модели. Однако для логических моделей характерен ряд сомнительных моментов, а поскольку большинство исследователей в области искусственного интеллекта – люди с неформальным мышлением, то большая часть достижений в области систем с базами знаний до недавнего времени принадлежала так называемой группе исследователей нелогического направления. В отличие от исследователей логического направления, которые выбирают предметом своих исследований сравнительно простые задачи, для решения которых используются теоретические подходы, исследователи нелогического направления выбирают сложные задачи и пытаются сконцентрировать все внимание на развитии способностей. Кроме того, в отличие от первой категории исследователей, которые почти не занимаются теоретическими исследованиями, вторая категория придает им большое значение. Другими словами, так называемая “человеческая логика” – это интеллектуальная модель с нечеткой структурой – в этом ее отличие от строгой логики. Более точно следует сказать, что исследователи логического направления ищут пути логического решения (в малой модели) задач, поставленных исследователями нелогического направления, и постепенно расширяют рамки логики. Примерами тому являются модальная логика, многозначная логика и т.п. В 80-х гг. было пересмотрено отношение к преимуществам и значимости логических методов, и они в различных формах стали применяться в нелогических моделях представления знаний. Это обусловлено, с одной стороны, необходимостью в точном представлении знаний, а с другой – ставшими очевидными пределами традиционных систем знаний, чрезмерно тяготеющих к эвристике.
3.2 Продукционная модель представления знаний
В модели правил знания представлены совокупностью правил вида “ЕСЛИ – ТО”. Системы с базами знаний, основанные на этой модели, называются продукционными системами. Эти системы бывают двух диаметрально противоположных типов – с прямыми и обратными выводами. Типичным представителем первого типа является система MYCIN, используемая для решения задач диагностического характера, а типичным представителем систем второго типа – OPS, используемая для решения проектирования задач.
В системе продукций с обратными выводами с помощью правил строится дерево И/ИЛИ, связывающее в единое целое факты и заключения; оценка этого дерева на основании фактов, имеющихся в базе данных, и есть логический вывод. Логические выводы бывают прямыми, обратными и двунаправленными. При прямом выводе отправной точкой служат предоставленные данные, процесс оценки приостанавливается в узлах с отрицанием, причем в качестве заключения (если не все дерево пройдено) используется гипотеза, соответствующая самому верхнему уровню дерева (корню). Однако для такого вывода характерно большое количество данных, а также оценок дерева, не имеющих прямого отношения к заключению, что излишне. Преимущество обратных выводов в том, что оцениваются только те части дерева, которые имеют отношение к заключению, однако если отрицание или утверждение невозможны, то порождение дерева лишено смысла. В двунаправленных выводах сначала оценивается небольшой объем полученных данных и выбирается гипотеза (по примеру прямых выводов), а затем запрашиваются данные, необходимые для принятия решения о пригодности данной гипотезы. На основе этих выводов можно реализовать более мощную и гибкую систему.


