Реферат: НАХОЖДЕНИЕ ВСЕХ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ АЛГЕБРАИЧЕСКОГО МНОГОЧЛЕНА МЕТОДОМ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ (БИСЕКЦИИ) И МЕТОДОМ ХОРД И КАСАТЕЛЬНЫХ С УКАЗАННОЙ ТОЧНОСТЬЮ И УЧЕТОМ ВОЗМОЖНОЙ КРАТНОСТИ КОРНЕЙ
x x в) г)
а) F’(x) < 0
F’’(x) > 0
б) F’(x) > 0
F’’(x) > 0
в) F’(x) < 0
F’’(x) < 0
г) F’(x) > 0
F’’(x) < 0
|
Способ хорд |
Способ касательных |
|
|
F’(x)F’’(x) > 0 |
С недостатком | С избытком |
|
F’(x)F’’(x) < 0 |
С ибытком | С недостатком |
Таким образом, если хорда (касательная) дает значение корня с избытком, то этот корень берется с качестве новой правой границы, а если с недостатком – то левой. В обоих случаях точный корень лежит между точками пересечения хорды и касательной с осью абсцисс.
Замечание 2 к методу хорд и касательных. Так как для решения поставленной задачи требуется отыскание производной функции F(x), метод хорд и касательных достаточно трудно реализуем на программном уровне, т.к. правила вычисления производных в общем виде довольно громоздки для «понимания» ЭВМ; при непосредственном указании производной для каждой степени многочлена память компьютера серьезно загружается, что очень замедляет работу, а задание функции и, соответственно, ее производной непосредственно в программном коде – недопустимо. Однако, используя данный метод, сходимость интервала к корню происходит наиболее быстро, особенно если совместить метод хорд и касательных с методом бисекции, т.к. середина нового отрезка зачастую дает вполне удовлетворительное решение.
2.2.2. Метод итераций
Пятый шаг алгоритма хорд и касательных определял возврат к первому шагу и последующую цикличность хода, т.е. метод хорд и касательных являлся итерационным. Другой метод, также основанный на повторах так и был назван – «метод итераций». Суть его заключается в следующем:
- дана функция F(x);
- определена допустимая погрешность Q;
- определен некоторый интервал [ a , b ], точно содержащий решение уравнения.
- Определено некоторое число z, принадлежащее [ a , b ] (назовем z «нулевым приближением»)
Для получения следующего приближения подставим в формулу (1) вместо X Z, получим:
x1=F(z) (4)
и, продолжая аналогично,
x2=F(x1)
x3=F(x2)
(5)
…
xn=F(xn-1)
Таким образом, получаем некоторую последовательность, и, если ее предел (6)
limxn=A, n®v (6)
то А является искомым корнем.
Данный метод является исключительно аналитическим, что упрощает его машинную реализацию, однако содержит следующие недостатки:
- необходимость выбора нулевого приближения (ведь то, что интуитивно для человека, для ЭВМ может стать довольно сложной задачей)
- наконец, полученная последовательность просто может не сходиться, и тогда решение найдено не будет.
Эти контраргументы стали основанием для отклонения метода итераций при выборе алгоритмизируемого метода.
2.2.3. Метод половинного деления (метод бисекции)
 |
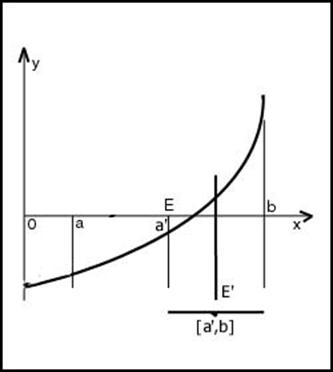рис.2
Метод половинного деления (известный еще и как «метод деления отрезка пополам») также является рекурсивным, т.е. предусматривает повторение с учетом полученных результатов.
Суть метода половинного деления заключается в следующем:
- дана функция F(x);
- определена допустимая погрешность Q;
- определен некоторый интервал [ a , b ], точно содержащий решение уравнения.
1. Вычисляем значение координаты Е, беря середину отрезка [a , b], т.е. Е= (a + b ) / 2 (7)
2. Вычисляем значения F(a), F(b), F(E), и осуществляем следующую проверку: Если F(E)>Q, то корень с указанной точностью найден. Если F(E)<Q, т.е. необходимая точность еще не достигнута, то формируем два интервала: [a , E] и [E , b] проверяем знаки F(a), F(b), F(E). На концах одного из этих интервалов знаки функции будут одинаковы, а на друго различны (иначе Е - искомый корень). И именно то интервал, на концах которого знаки различны, мы берем за основу при следующей итерации, т.е. приравниваем к Е либо a, либо b.
3. Переходим к пункту 1.
Задачу можно упростить, если определить границы корней: граница абсолютных значений корней вычисляется по формуле (8)
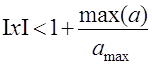
: (8),
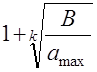(9),
границу положительных корней – по формуле (9):
а границу отрицательных корней – заменив в уравнении (1) х на –х.
Таким образом, мы получаем метод, хотя и достаточно медленный (впрочем, при неудачном выборе нулевого приближения в методе итераций поиск решения может затянуться на еще более долгое время, да и к тому же неизвестно, приведет ли весь ход вычислений к ответу), но зато вполне надежный и простой метод, не требующий решения дополнительных задач, вроде вычисления производной, а рекурсивность самого алгоритма позволяет получить очень компактный и легко читаемый код. Именно поэтому метод половинного деления и был выбран для реализации на программном уровне.
2.2.4. Метод разложения на множители
Данный метод является полностью аналитическим, однако полностью зависим от других. Главным его преимуществом является то, что в данном методе не происходит потери кратных корней. Поясним на примере:
Пусть дан многочлен F(x) = 2x3-11x2+20x-12 (11)
Его можно записать в виде: F(x) = (x+2)2(2x-3) (12)
У многочлена n-степени, как известно, n корней, а из (12) следует, что корнями F(x) являются –2 и 1,5, причем корень –2 является кратным, т.е. фактически это два одинаковых корня. При отыскании же корней любым из вышеописанных методов «второй» корень –2 будет потерян, т.к. график функции будет иметь лишь две точки пересечения с осью абсцисс
Чтобы избежать этого применяется метод разложения на множители. Суть его заключается в следующем: каждый многочлен вида (1) можно представить в виде (x+h1)(x+h2)…(x+hn)*H = 0 (13) ,
или F(x) = (x+h)(bn-1xn-1+…b1)+b0 (14)
где h1…hn – корни уравнения, а Н – произведение множителей х, вынесенных за скобки ( Н никак не влияет на уравнение, т.к. от него избавляются, деля на Н обе части (13). При этом не исключено, что некоторые h могут быть взаимно равны, что и свидетельствует о наличии кратного корня.
Для вычисления значений новых коэффициентов в (14) используются формулы:
bn=an
bn-1=bnh+an-1 (15)
bn-2=bn-1h+an-2
…
Таким образом, алгоритм этого метода выглядит следующим образом:
1. Определить границы корней уравнения;
2. При помощи любого из вышеописанных методов найти один корень уравнения;
3. Применяя формулы (14) и (15) сформировать новый многочлен степени, на 1 меньшей предыдущего.
4. Вернуться к пункту 2.
5. Повторять до тех пор, пока степень многочлена не обнулится.
Этот метод был реализован на программном уровне и включен в курсовую работу.
3. ОПИСАНИЕ СТРУКТУРЫ ПРОГРАММЫ
В рамках задания на курсовую работу в среде программирования Visual Basic for Applications была разработана программа, находящая корни многочлена с указываемой точностью.
3.1. Описание программных модулей
