Реферат: Вязкость при продольном течении

Для того, чтобы получить отсюда значение напряжения σ11 надо воспользоваться равенством σii=-p+σ’i и, пренебрегая силами поверхностного натяжения, записать, что

Исходя из первого уравнения системы (1.11) следует,что гидростатическое давление (отнюдь не равное внешнему) выражается через градиент скорости

Исходя из первого уравнения системы (1.11), можно получить

Отсюда следует, что продольная вязкость при растяжении выражается как функция градиента скорости

                                                                 (1.12)

Теория предсказывает, что при низких продольных градиентах скорости растяжения (при έ0«1/θ) значение λ=Зη=λ0, но при возрастании градиента скорости продольная вязкость монотонно увеличивается, и при έ0—> θ/2 продольная вязкость неограниченно возрастает: λ—>∞. При градиентах скорости, больших θ/2,установившееся течение при растяжении вообще оказывается невозможным.

Рассмотрим случай одноосного сжатия, по кинематике обратный одноосному растяжению. Для обычной вязкой жидкости при замене растяжения сжатием все реологические характеристики среды (с точностью до знака) остаются неизменными. Но для вязкоупругой среды сжатие не является процессом, обратным растяжению. Это видно из приведенных ниже соотношений. Сжатию отвечает тензор скоростей деформации

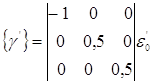
поэтому уравнения (1.11) заменяются следующей системой:

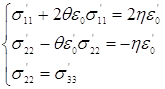
                                                                                   (1.13)

Повторяя все вычисления, проделанные для деформации одноосного растяжения, и определяя вязкость при сжатии λ точно так же, как при любых других режимах деформации отношением (σ11/έ0) можно найти, что

                                                                          (1.14)

Таким образом, для модели (1.10), обобщенной на большие деформации по Олдройду, вязкость при растяжении λ, оказывается не равной вязкости при сжатии λ,. Этот результат показывает, что в принципе для вязкоупругой жидкости с произвольными реологическими свойствами, несмотря на кинематическую обратимость растяжения и сжатия, может иметь место неравенство: λ=λ,.

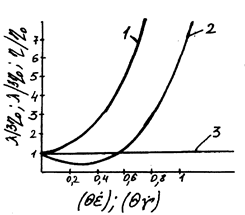
Вязкоупругая жидкость, реологические свойства которой описываются уравнением (1.10) с производной в смысле Олдройда, не проявляет аномалии вязкости при сдвиге, то общая картина изменения «вязкостей» этой жидкости в зависимости от градиента скорости при трех рассмотренных схемах деформации в режиме установившегося течения оказывается такой, как показано на рис. 1.2.

Таким образом, жидкость, не проявляющая аномалии вязкости при сдвиговом течении, обнаруживает эффект возрастания вязкости

Рис 1.2. Изменение вязкости вязкоупругои

"олдройдовской" жидкости с одним временем

релаксации в зависимости от скорости

деформации:

1 - продольная вязкость при растяжении λ/3η0;

2 - продольная вязкость при сжатии λ/3η0;

3 - вязкость при сдвиговом течении η/η0.

при растяжении вследствие развивающихся высокоэластических деформаций.

Эффект аномалии вязкости при сдвиговом течении естественным образом описывается при использовании реологического уравнения (1.9), обобщенного на случай больших деформаций с помощью яуманновской производной. Но для одноосного растяжения эта модель не предсказывает возникновения каких-либо новых эффектов, отличных от тех, которые известны для чисто вязкой жидкости, т. е. для такой вязкоупругой среды                                 

Этот вывод физически обусловлен тем, что эффект аномалии вязкости в яуманновской модели возникает из-за вращения координатной системы, связанной с данной точкой, при деформировании среды. При однородном одноосном растяжении вращение элементов тела отсутствует, и поэтому вязкоупругая среда ведет себя как ньютоновская жидкость.

Таким образом, использование яуманновской производной не дает возможности высказать какие-либо правдоподобные суждения о характере реологического поведения вязкоупругой среды при растяжении. Поскольку олдройдовская производная не позволяет сделать этого относительно сдвигового течения, то очевидно, что обе эти модели не могут одновременно правильно описать реологические свойства вязкоупругой жидкости и при растяжении и при сдвиге, и поэтому в общем случае они оказываются неадекватными реальным свойствам вязкоупругой среды.

Из более сложных моделей вязкоупругих сред целесообразно остановиться на модели Сприггса, представляющей собой модель вязкоупругой жидкости с известным релаксационным спектром, обобщенную на случай больших деформаций с помощью дифференциального оператора довольно сложного строения.

При кинематике движения, отвечающей одноосному растяжению продольная вязкость λ оказывается равной :

                                                                                  (1.15)

где α—показатель, характеризующий частоту распределения времен релаксации в спектре; θт — максимальное время релаксации; ζ(α) — дэета-функция Римана.

Из этой модели непосредственно вытекают некоторые частные случаи, представляющие интерес. Если ε=-1, что отвечает модели де-Уитта,то λ=3η как это уже было получено выше. Если ε=0, что отвечает обобщенной (нелинейной) модели Олдройда, то формула (1.15) предсказывает рост продольной вязкости при увеличении градиента скорости, по характеру такой же, как это имело место и при использовании линейного оператора Олдройда. Однако в этой модели рост продольной вязкости сопровождается снижением эффективной вязкости при сдвиговом течении. Это показывает, что существуют такие способы обобщения реологических уравнений состояния линейных вязкоупругих сред, которые правильно описывают поведение жидкости и при растяжении в при сдвиге одновременно.

Изложенные выше результаты применения реологических моделей вязкоупругих сред для анализа продольного течения относились к системам, у которых релаксационный спектр и, следовательно, их вязкоупругие свойства не зависят от интенсивности деформирования. Между тем, как это хорошо известно для сдвигового деформирования, возрастание интенсивности воздействия приводит к изменению релаксационных свойств системы. Этот же эффект должен наблюдаться и при растяжении, поскольку коэффициент вязкости, входящий во все формулы для продольной вязкости, уменьшается ври возрастании интенсивности механического воздействия на систему.

Количественной характеристикой влияния интенсивности воздействия на коэффициент η является его зависимость от второго инварианта Т2 тензора скоростей деформаций. При растяжении

и при сдвиге

Поэтому условие эквивалентности интенсивности воздействия на материал при сдвиге и растяжении выполняется, если

                                                                     (1.16)

Тогда в общем случае зависимость продольной вязкости при растяжении λ от градиента скорости έо должна представляться в виде :

                                                                                                                      (1.17)

где f(έo) — возрастающая функция.

Эта функция отражает влияние ориентации полимера, приводящей к усилению межмолекулярного взаимодействия, на вязкость. Некоторые примеры этой функции, следующие из различных реологических моделей, приводились выше.

Функция η(έ0,) входящая в выражение для продольной вязкости, является аналогом зависимости эффективной вязкости при сдвиге от скорости деформации с учетом указанного различия между зависимостью T2 от γ’ или έ [см. формулу (1.16)]. Эта функция отражает влияние деформаций на разрушение структурных связей, приводящее к частичному подавлению медленных релаксационных процессов (усечению спектра со стороны больших времен релаксации) и, как следствие этого, к снижению эффективной вязкости по мере возрастания скорости деформации.

Экспериментально наблюдаемая зависимость эффективной вязкости при растяжении от продольного градиента скорости λ(έ0) определяется наложением двух процессов — ориентации и частичного изменения релаксационного спектра материала. По-видимому, совершенно аналогичные явления происходят и при сдвиге. Но при растяжении, как общее правило, доминирует процесс ориентации, что приводит к возрастанию (см. ниже) функции λ(έо), в то время как при сдвиге обычно доминирует эффект, который можно трактовать как разрушение структуры системы. Это обусловлено тем, что при сдвиге направления ориентации и деформации не совпадают, а при растяжении — совпадают.

Предельные значения рассматриваемых функций равны:

Поэтому в области низких скоростей сдвига выполняется «закон Трутона», согласно которому

Величину         называют начальной (трутоновской) вязкостью системы.

3.3. Продольная вязкость растворов (молекулярные

модели).

Рассмотрение теории продольного течения разбавленных растворов полимеров (хотя такой режим течения очень трудно реализовать практически) позволяет судить о том, в какой мере собственные вязкоупругие свойства макромолекулы могут явиться первопричиной особенностей поведения полимерных систем при одноосном растяжении. Этот вопрос аналогичен тому, который рассматривался при анализе вязкоупругих свойств индивидуальных полимерных цепочек при сдвиговом деформировании, когда реологические свойства системы объяснялись, исходя из релаксационного спектра отдельных макромолекул, движение которых складывается из независимых смещений. Этот подход состоит по существу, в построении физической модели полимерной системы и рассмотрении того, как такая модель ведет себя при сдвиге и при растяжении.

Простейшей формой частиц, которые могут ориентироваться в потоке, являются эллипсоиды. Поэтому поведение суспензии жестких эллипсоидов при течении в поле скоростей с продольным или поперечным градиентом позволяет установить влияние фактора ориентации на характер зависимостей η(у’) и λ(έ). На каждую частицу в потоке действуют силы вязкого трения окружающей среды и силы, обусловленные броуновским движением самой частицы. Под действием градиента скорости частицы стремятся ориентироваться в потоке строго определенным образом, броуновское движение служит дезориентирующим фактором. В результате в стационарном потоке устанавливается некоторое равновесное распределение ориентации осей частиц, которое зависит как от собственных свойств частиц (их размеров, формы и коэффициента диффузии), так и от градиента скорости. Совокупность вязких потерь при деформировании такой суспензии определяется распределением ориентации осей частиц относительно направления градиента скорости. Различие в распределении ориентации возможно только, если частицы обладают анизодиаметричностъю формы; в суспензии сферических частиц все направления скорости не изменяет структуры системы.

Существенно, что равновесное распределение ориентации эллипсоидов в потоке зависит от геометрий потока . При этом функция η(έ0) — убывающая, но функция λ(έ0) оказывается возрастающей, и ее вид зависит от соотношения между свойствами частиц и градиентом скорости. Этот теоретический результат показывает, что система, реологические свойства которой при сдвиге характеризуются аномалией вязкости (эффективная вязкость уменьшается с возрастанием скорости деформации), может при растяжении вести себя так, что с увеличением градиента скорости продольная вязкость возрастает.

Таким образом, даже простейшая модель суспензии жестких эллипсоидов позволяет качественно предсказать принципиальное различие в поведении полимерной системы при сдвиговом течении при растяжении и показывает, что связь между эффективной вязкостью при сдвиге и при растяжении может быть в достаточной мере сложной и неоднозначной.

В более реалистической модели полимерной системы макромолекула представляется в виде вязкоупругой нити или пористого клубка со статистическим распределением сегментов относительно центра масс. Эффективная вязкость модели в рамках линейной теории вязкоупругости не зависит от скорости сдвига. Если проанализировать реологические свойства молекулярной модели при одноосном растяжении, то оказывается, что следует ожидать возрастания продольной вязкости с увеличением градиента скорости. Точный вид зависимости λ(ε) определяется числовыми значениями параметров модели.

Возрастание продольной вязкости при увеличении градиента скорости при растяжении вязкоупругого пористого клубка является следствием двух факторов — ориентационного механизма, аналогичного описанному выше для суспензии жестких эллипсоидов (но с той разницей, что анизотропия молекулярного клубка — вынужденная, создаваемая самим градиентом скорости и являющаяся в этом смысле «деформационной анизотропией»), и релаксационного механизма, связанного с большими деформациями вязкоупругой среды и аналогичного тому, который приводит к возрастанию вязкости максвелловской жидкости с одним временем релаксации при больших деформациях. Количественные предсказания теории продольного течения суспензии вязкоупругих статистических клубков зависят от выбора модели самого клубка и от способа учета больших упругих деформаций. Поэтому теоретические результаты оказываются неоднозначными, хотя, в принципе, они позволяют объяснить и описать наблюдаемый характер функции λ(έ), исходя из представлений о релаксационном спектре среды.

Молекулярные модели типа моделей КСР и КРЗ — это модели вязкоупругих сред с дискретным распределением времен релаксации θР. Характер изменения продольной вязкости λ при растяжении для среды с одним временем релаксации, с учетом больших деформаций по Олдройду, предсказывается формулой (1.14). Наложение различных релаксационных механизмов приводит к суммированию вкладов каждого из них в продольную вязкость. Поэтому для модели пористого клубка с релаксационным спектром θР (при учете больших деформаций с помощью оператора Олдройда) зависимость λ(έ) имеет вид (по Р.Берду с соавторами)

                                                                             (1.18)

где N0 — число цепей в единице объема; k— постоянная Больцмана; Т — лютная температура; η0 — наибольшая (начальная) ньютоновская вязкость при сдвиговом течении.

Аналогия структуры формул (1.14) и (1.18) очевидна. Однако эта модель не предсказывает эффекта аномалии вязкости при сдвиговом течении, хотя при простом сдвиге этой модели отвечает возникновение нормальных напряжений, пропорциональных ў2.

Молекулярные модели приводят практически к тем же количественным результатам, что и собственно феноменологические модели с той лишь разницей, что константам, входящим в итоговые формулы придается определенный физический смысл. Этот результат естественен, поскольку молекулярные модели оперируют теми же исходными понятиями и представлениями, что и феноменологические модели. Важнейшими из них являются: во-первых, понятие о релаксационном спектре системы и влиянии интенсивности деформирования на релаксационные свойства системы и, во-вторых, способ перехода от конвективной системы координат к неподвижной. Первое учитывает специфику реакции полимерной системы на внешнее воздействие как вязкоупругой релаксаций; второе — геометрические эффекты, обусловленные большими упругими деформациями среды Сочетанием этих факторов определяются практически все наблюдаемые или теоретически рассматриваемые особенности реологических свойств полимерных систем в любых режимах деформирования. В зависимости от геометрии деформации (например, при растяжении или при сдвиге) взаимное влияние этих факторов может быть различным, что приводит к различиям в проявлении реологических свойств системы в зависимости от схемы деформирования.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1.Виноградов Г. В., Малкин А. Я. Реология полимеров. М., "Химия", 1977

2.   Торнер Р. В. Теоретические основы переработки полимеров (механика
процессов). М., "Химия", 1977.