Быстрый поиск

Реферат: Сетевое моделирование при планировании. Задача о коммивояжере...

Исходная матрица

Решение

x3 = 1

x5 = 1

x7 = 1

x8 = 0

x11 = 1

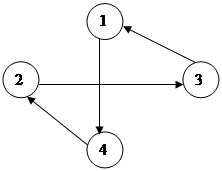
Это означает, что на графике остаются только пути, соответствующие переменным х3, х5, х7, х11 (1 4, 2 3, 3 1, 4 2). Функционал равен 12, т. е. время пути будет равно 12 единицам. График при этом выглядит следующим образом.

Задание №3

Тема: Графы

Задача о максимальном потоке

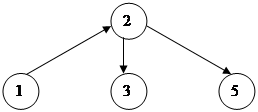
Имеется трубопроводная сеть с заданной Sij пропускной способностью каждого участка из i-го узла в j-й узел и мощностью насосной станции, расположенной в узле. Необходимо рассчитать максимальную пропускную способность сети из начального узла в конечный узел.

aисток aсток

Пропускная способность Sij , тыс. тонн

S12 = 4

S13 = 7

S14 = 8

S23 = 3

S25 = 5

S34 = 8

S35 = 9

S45 = 9

Математическая модель

Обозначим за х1, 2, …, 8 перевозки по маршрутам 12, 13, 14, 23, 25, 34, 35, 45 соответственно, а за х9 – пропускную способность конечного узла сети.

Сумма входящих в каждый узел потоков равна сумме выходящих, причем интенсивность каждого потока не может превышать пропускную способность своего участка сети. Поэтому система условий-ограничений выглядит следующим образом.

х9 - х1 – х2 – х3 = 0 (1)

х1 – х4 – х5 = 0 (2)

х2 + х4 – х6 – х7 = 0 (3)

х3 + х6 – х8 = 0 (4)

х5 + х7 + х8 – х9 = 0 (5)

х1 £ 4 (6)

х2 £ 7 (7)

х3 £ 8 (8)

х4 £ 3 (9)

х5 £ 5 (10)

х6 £ 8 (11)

х7 £ 9 (12)

х8 £ 9 (13)

Функция цели: х9 max

Таблица 3.1

Исходная матрица

№	х1	х2	х3	х4	х5	х6	х7	х8	х9	Знак	Св.чл.
1	-1	-1	-1	0	0	0	0	0	1	=	0
2	1	0	0	-1	-1	0	0	0	0	=	0
3	0	1	0	1	0	-1	-1	0	0	=	0
4	0	0	1	0	0	1	0	-1	0	=	0
5	0	0	0	0	1	0	1	1	-1	=	0
6	1	0	0	0	0	0	0	0	0	£	4
7	0	1	0	0	0	0	0	0	0	£	7
8	0	0	1	0	0	0	0	0	0	£	8
9	0	0	0	1	0	0	0	0	0	£	3
10	0	0	0	0	1	0	0	0	0	£	5
11	0	0	0	0	0	1	0	0	0	£	8
12	0	0	0	0	0	0	1	0	0	£	9
13	0	0	0	0	0	0	0	1	0	£	9
Ф. ц.	0	0	0	0	0	0	0	0	1	max