Реферат: Решение обратных задач теплопроводности для элементов конструкций простой геометрической формы
Таким образом, имеем типичную некорректную задачу, для построения устойчивого решения которой необходимо построение регуляризирующих алгоритмов.
Сохраним в решении (3) конечное число слагаемых N. Введем обозначения
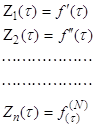(4)
Интегрируя (4) получим систему интегральных уравнений Вольтерра первого рода:
,
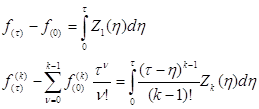(5)
где k =1, 2, ... , N.
Соотношения для теплового потока в (3) записывается аналогично. В дальнейшем будем считать, что на поверхности X = 0 теплосъем отсутствует, то есть стенка теплоизолирована. Тогда решение (3) с учетом обозначений (4) записывается в виде
(6)
Таким образом, граничные условия при X = 1 восстанавливаются соотношением (6),
в котором функции 
находятся из
решения интегральных уравнений (5)
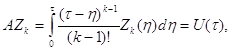(7)
где правая часть задается приближенно, то есть
Здесь
- числовой параметр,
характеризующий погрешность правой части уравнения (7).
Задача (7) является, в общем случаи некорректно поставленной /12/. Наиболее распространенным в настоящее время эффективным регуляризующим алгоритмом для ее решения является алгоритм, основанный на минимизации функционала А.Н.Тихонова /12/.
(8)
С
последующим выбором параметра регуляризации 
по
так называемому принципу невязки.
Например, если 
- какая - либо
экстремаль функционала (8), реализующая его глобальный минимум при заданном 
и фиксированном 
, то числовой параметр
определяется из условия
(9)
Регуляризующий алгоритм (7) - (9) подробно изучен в /12/ и обладает устойчивостью к малым возмущениям правой части (7).
Правая часть уравнения (7) при решении формировалась следующим образом.
Функция 
характеризующая изменение
температуры поверхности, задавалась таблицей. Начальные условия для 
1, 2, … , N-1) находились из
соотношения /3/:
(10)
где
, 
- распределение
температуры, заданное в начальный момент времени. Откуда для равномерного
распределения температуры в начальный момент времени имеет
1, 2, … ,
N-1
(11)
Из анализа теплофизических и геометрических характеристик конструкции камеры сгорания следует возможность представления системы пластин теплового отношения (рис.1) в виде пластины из теплозащитного покрытия и оболочки, которую можно рассматривать как тепловую емкость. Это дает возможность воспользоваться для построения решения обратной тепловой задачи для заданного узла решением задачи Коши (3). В системе координат, представленной на Рис.1, поверхность при X = 0 будем считать теплоизолированной, то есть
(12)
Кроме этого предположим, система
пластин в начальный момент времени прогрета равномерно и, следовательно,
начальные условия для функции 
имеют
вид (11).
При сделанных выше предположениях условия Коши (12) для этой задачи имеют вид
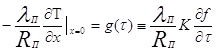(13)
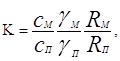Где
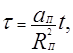
Подставляя значение 
из условия (2) в решение
задачи Коши (3) получим
(14)
где
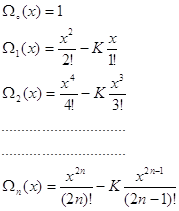
Таким образом, решение этой задачи имеет вид
(15)
где 
нам
задана, а функции 
(n=1,
2, … , N)
определяются из
решения
интегральных уравнений Вольтерра первого рода (5) методом регуляризации
(7) - (9).
Следовательно, искомые величины
определяются
из решения (4) с использованием регуляризирующего алгоритма (7) - (9).
Метод наименьших квадратов.
Пусть функция 
задана
на 
своими значениями в точках 
. Рассмотрим совокупность
функций
(16)
линейно независимых на 
.
Будем отыскивать линейную комбинацию этих функций
(17)
так, чтобы сумма квадратов ее отклонений от заданных значений 
функции в узлах 
имела бы наименьшее
возможное значение, то есть величина
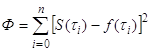(18)
принимала бы минимальное значение.
Заметим, что упомянутая сумма является функцией коэффициентов
.
(19)
