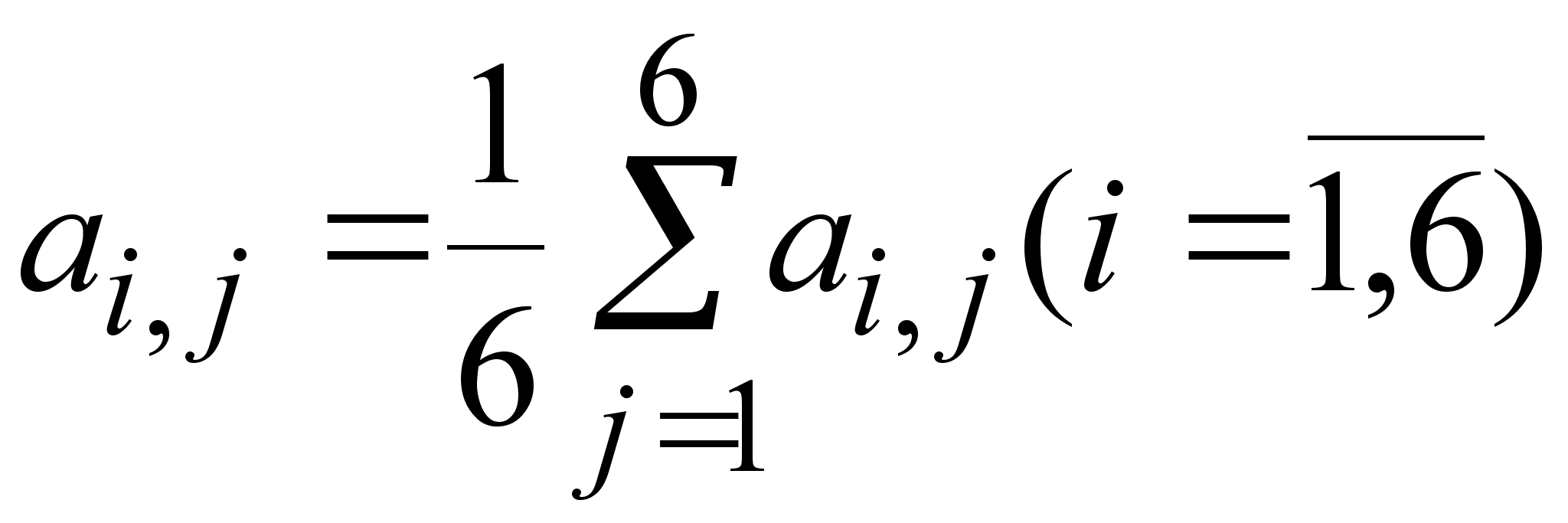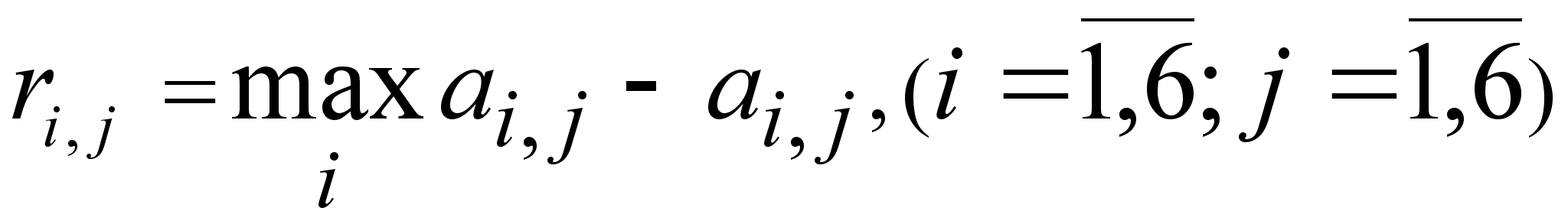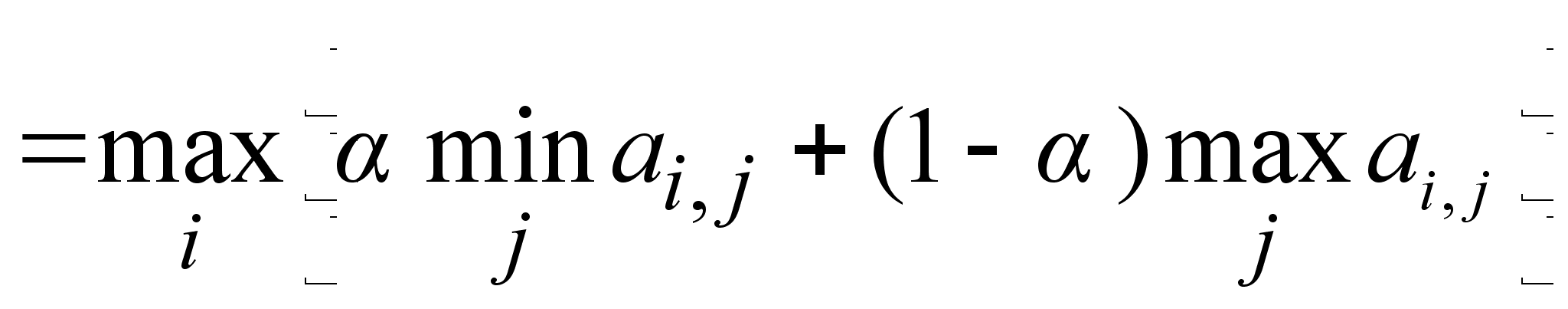Реферат: Определение стратегии руководства перерабатывающего предприятия по сезонному набору силы с учетом различного объема перерабатывающего сырья
Реферат: Определение стратегии руководства перерабатывающего предприятия по сезонному набору силы с учетом различного объема перерабатывающего сырья
Министерство сельского хозяйства и продовольствия Республики Беларусь
БЕЛОРУССКИЙ АГРАРНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра информационных процессов и технологий
Курсовая работа
На тему: "Определение стратегии руководства перерабатывающего предприятия по сезонному набору силы с учетом различного объема перерабатывающего сырья.”
Курсовая работа №4 Вариант №3
МИНСК 2000
CОДЕРЖАНИЕ
1.Постановка задачи-----------------------------------------------3стр.
2.Игровая схема задачи-------------------------------------------4стр.
3.Платежная матрица задачи------------------------------------4стр.
4.Решение в чистых стратегиях---------------------------------4стр.
5.Расчет оптимальной стратегии по критериям:
а) Байеса------------------------------------------------------------5стр.
б) Лапласа----------------------------------------------------------5стр.
в) Вальда------------------------------------------------------------5стр.
г) Сэвиджа----------------------------------------------------------6стр.
д) Гурвица----------------------------------------------------------6стр.
6.Задача линейного программирования-------------------------6стр.
7.Программа (листинг)----------------------------------------------8стр.
8.Решение задачи, выданное программой----------------------10стр.
9.Вывод----------------------------------------------------------------10стр.
1. ПОСТАНОВКА ЗАДАЧИ.
Определение стратегии руководства перерабатывающего предприятия по сезонному набору силы с учетом различного объема перерабатывающего сырья.
Консервный
завод производит
дополнительный
набор рабочей
силы осенью
в период интенсивной
переработки
продукции
(сырья). Потребность
в рабочих
определяется
уровнем производства
с.х. продукции
(сырья) и составляет
,
человек Расходы
на зарплату
одного человека
,
а расходы в
сезон составляют
,
.
Уволить невостребованный
рабочих можно,
выплатив им
30% средств, положенных
им по контракту.
A1=20 B1=40 q1=0,1
A2=21 B2=46 q2=0,25
A3=22 B3=50 q3=0,15
A4=23 B4=54 q4=0,25
A5=27 B5=56 q5=0,15
A6=28 B6=60 q6=0,1
d=36 =0,7
Требуется:
1) придать описанной ситуации игровую схему, установить характер игры и выявить ее участников, указать возможные стратегии сторон;
2) вычислить элементы платежной матрицы;
3) для игры с полученной платежной матрицей найти решение в чистых стратегиях (если оно существует), вычислив нижнюю и верхнюю чистую цену игры, в случае отсутствия седлового элемента определяется интервал изменения цены игры;
4) дать обоснованные рекомендации по стратегии найма рабочей силы, чтобы минимизировать расходы при предложениях:
а) статистические
данные прошлых
лет показывают,
что вероятности
,
уровней производства
с.х. продукции
известны;
б) достоверный прогноз об урожае отсутствует;
В пункте 4 необходимо найти оптимальные чистые стратегии, пользуясь в 4 а) критерием Байеса, в пункте 4 б) критериями Лапласа. Вальда, Сэвиджа, Гурвица.
5) для игры с данной платежной матрицей составить эквивалентную ей задачу линейного программирования и двойственную ей задачу, решить на ПЭВМ одну из задач и выполнить экономический анализ полученного оптимального плана (решения в смешанных стратегиях);
6) составить программу для нахождения оптимальной стратегии игры с произвольной платежной матрицей, используя один из критериев;
7) по составленной программе вычислить оптимальную стратегию для решаемой задачи.
2.Игровая схема задачи
Э
то
статистическая
игра. Один
игрок-Директор
завода (статистик),
второй игрок-природа.
Природа располагает
стратегиями
Пj
(j=1,6), какой будет
урожай. Директор
может использовать
стратегии Аi
(i=1,6), сколько рабочих
нанять.
3.Платежная матрица игры.
Платежная матрица игры имеет вид:
|
Природа |
1 |
2 |
3 |
4 |
5 |
6 |
|
Директор |
||||||
|
1 |
-720 |
-766 |
-820 |
-882 |
-1112 |
-1200 |
|
2 |
-730,8 |
-756 |
-806 |
-864 |
-1092 |
-1176 |
|
3 |
-741,6 |
-766,8 |
-792 |
-846 |
-1072 |
-1152 |
|
4 |
-752,4 |
-777,6 |
-802,8 |
-828 |
-1052 |
-1128 |
|
5 |
-795,6 |
-820,8 |
-846 |
-871,2 |
-972 |
-1032 |
|
6 |
-806,4 |
-831,6 |
-856,8 |
-882 |
-982,8 |
-1008 |
Элементы матрицы рассчитываются по формуле:
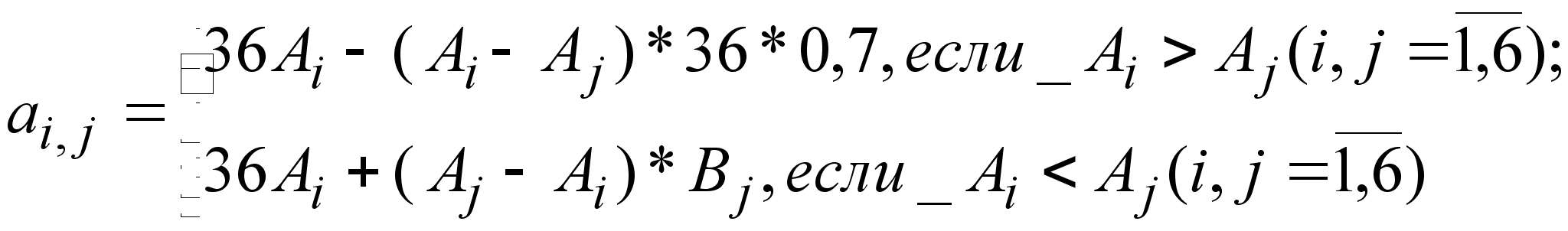
Например:
a2,3=-(36*21+(22-21)*50)=-806
a2,1=-(36*21-(21-20)*36*0,7)=-730,8
4.Решение в чистых стратегиях.
Вычисляем мин. выигрыш Директора, какую бы стратегию не применила природа, и макс. проигрыш природы, какую бы стратегию не применил Директор. В этом случае наша матрица примет вид:
|
Природа |
1 |
2 |
3 |
4 |
5 |
6 |
Мин выигрыш Директора |
|
Директор |
|||||||
|
1 |
-720 |
-766 |
-820 |
-882 |
-1112 |
-1200 |
-1200 |
|
2 |
-730,8 |
-756 |
-806 |
-864 |
-1092 |
-1176 |
-1176 |
|
3 |
-741,6 |
-766,8 |
-792 |
-846 |
-1072 |
-1152 |
-1152 |
|
4 |
-752,4 |
-777,6 |
-802,8 |
-828 |
-1052 |
-1128 |
-1128 |
|
5 |
-795,6 |
-820,8 |
-846 |
-871,2 |
-972 |
-1032 |
-1032 |
|
6 |
-806,4 |
-831,6 |
-856,8 |
-882 |
-982,8 |
-1008 |
-1008 |
|
Макс проигрыш Природы |
-720 |
-756 |
-792 |
-828 |
-972 |
-1008 |
Нижняя чистая цена игры=-1008
Верхняя чистая цена игры=-1008
Седловая точка=-1008
Стратегия A6 оптимальна для Директора, стратегия П6 —для природы.
5.Расчет оптимальной стратегии по критериям:
а) Байеса
статистические данные показывают, что вероятности различных состояний погоды составляют соответственно qi=1,6;
|
qi |
ai |
| 0.1 | -893,8 |
| 0.25 | -880,38 |
| 0.15 | -872,16 |
| 0.25 | -867,66 |
| 0.15 | -878,46 |
| 0.1 | -885,78 |
| Критерий Байеса |
-867,66 |
П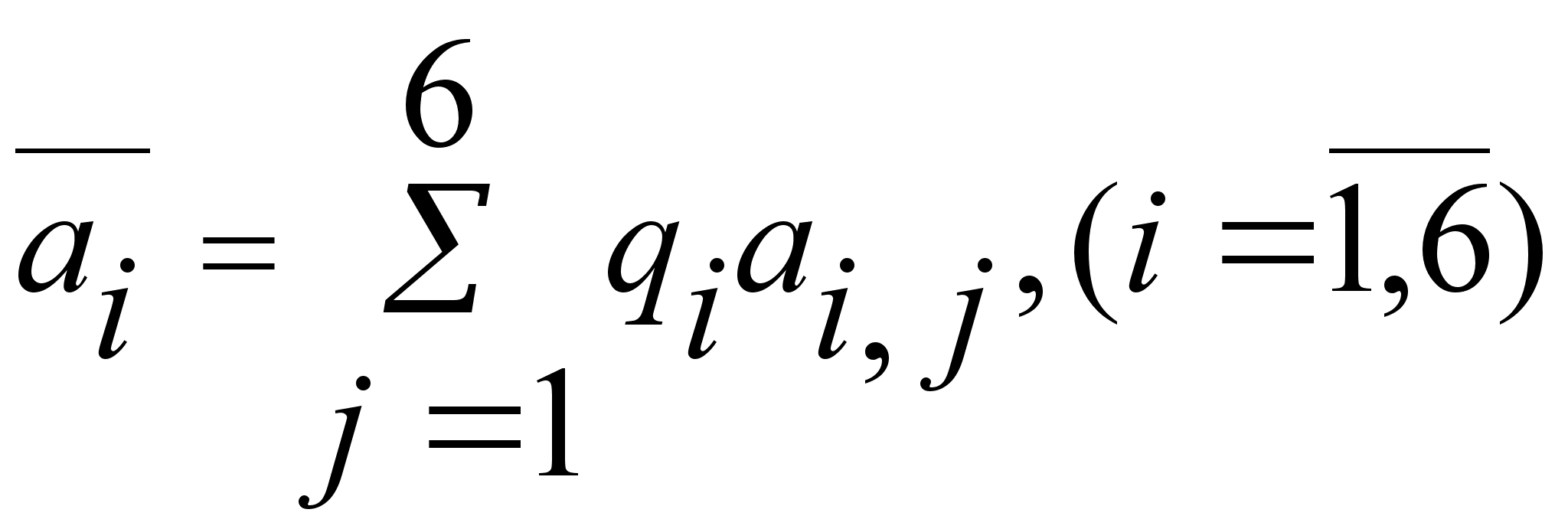
о
критерию Байеса
оптимальной
является четвертая
стратегия.
б) Лапласа
по критерию Лапласа вероятность наступления каждого из событий равновероятна.
|
a1= |
-916,67 |
|
a2= |
-904,13 |
|
a3= |
-895,07 |
|
a4= |
-890,13 |
|
a5= |
-889,60 |
|
a6= |
-894,60 |
|
К |
-889,6 |
По критерию Лапласа оптимальной является пятая стратегия.
в) Вальда
|
a1= |
-1200 |
|
a2= |
-1176 |
|
a3= |
-1152 |
|
a4= |
-1128 |
|
a5= |
-1032 |
|
a6= |
-1008 |
|
Критерий Вальда |
-1008 |
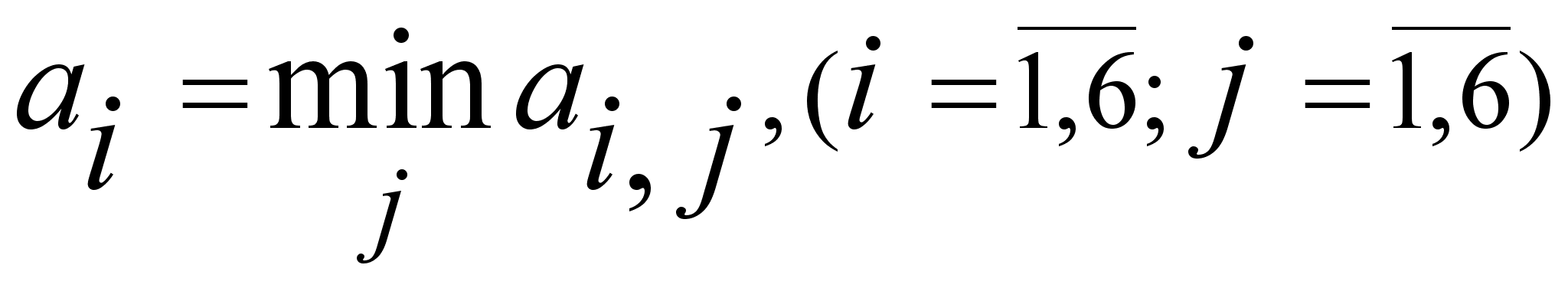
По критерию Вальда оптимальной является шестая стратегия .
г) Сэвиджа
Составим матрицу рисков:
|
1 |
2 |
3 |
4 |
5 |
6 |
ri |
|
|
1 |
0 |
10 |
28 |
54 |
140 |
192 |
192,00 |
|
2 |
10,8 |
0 |
14 |
36 |
120 |
168 |
168,00 |
|
3 |
21,6 |
10,8 |
0 |
18 |
100 |
144 |
144,00 |
|
4 |
32,4 |
21,6 |
10,8 |
0 |
80 |
120 |
120,00 |
|
5 |
75,6 |
64,8 |
54 |
43,2 |
0 |
24 |
75,60 |
|
6 |
86,4 |
75,6 |
64,8 |
54 |
10,8 |
0 |
86,40 |
|
К |
75,60 |
||||||
По критерию Сэвиджа оптимальной является пятая стратегия.
д) Гурвица
|
= |
0,7 |
|
A1 |
-1056 |
|
A2 |
-1042,44 |
|
A3 |
-1028,88 |
|
A4 |
-1015,32 |
|
A5 |
-961,08 |
|
A6 |
-947,52 |
|
Критерий Гурвица |
-947,52 |
Критерий Гурвица
По критерию Гурвица оптимальной является шестая стратегия.
6.Задача линейного программирования
Для того, чтобы составить задачу линейного программирования, приведём платёжную матрицу к положительному виду по формуле:
В результате
получаем следующую
таблицу:
| 0 | 46 | 100 | 162 | 392 | 480 |
| 10,8 | 36 | 86 | 144 | 372 | 456 |
| 21,6 | 46,8 | 72 | 126 | 352 | 432 |
| 32,4 | 57,6 | 82,8 | 108 | 332 | 408 |
| 75,6 | 100,8 | 126 | 151,2 | 252 | 312 |
| 86,4 | 111,6 | 136,8 | 162 | 262,8 | 288 |
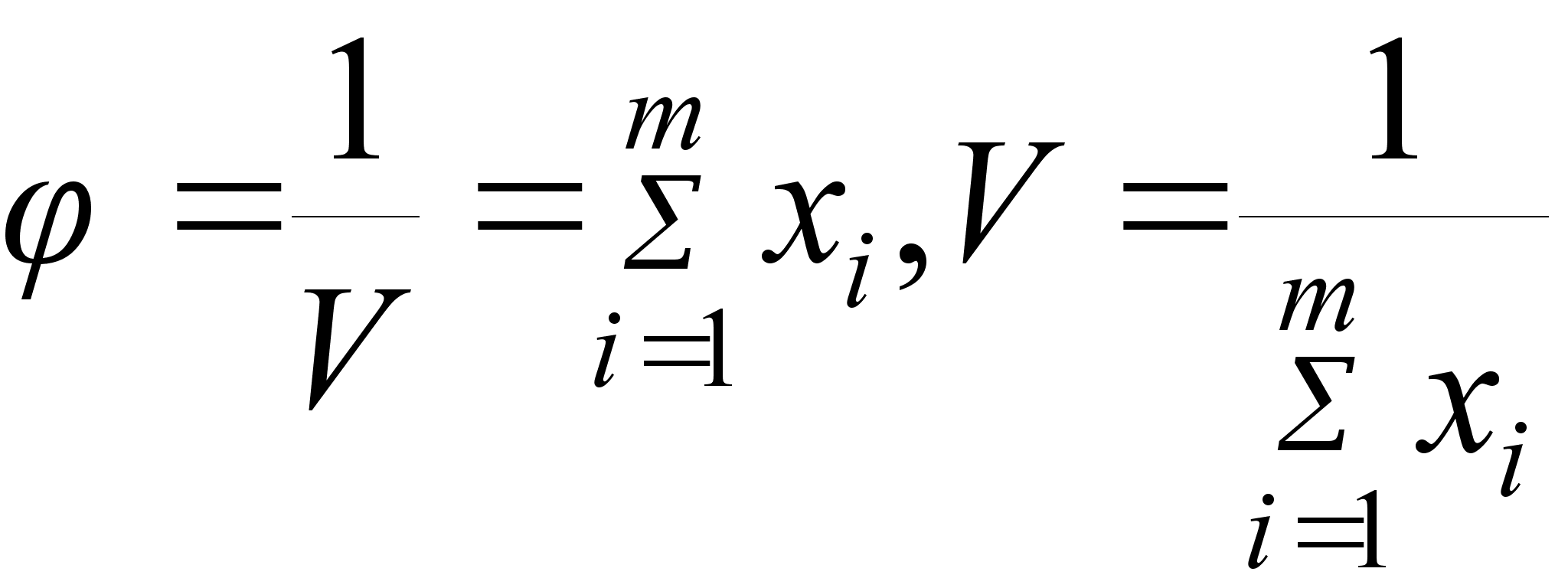
Игрок
A стремится
сделать свой
гарантированный
выигрыш V возможно
больше,
а значит возможно
меньше величину
φ
Учитывая данное соглашение, приходим к следующей задаче: минимизировать линейную функцию.
p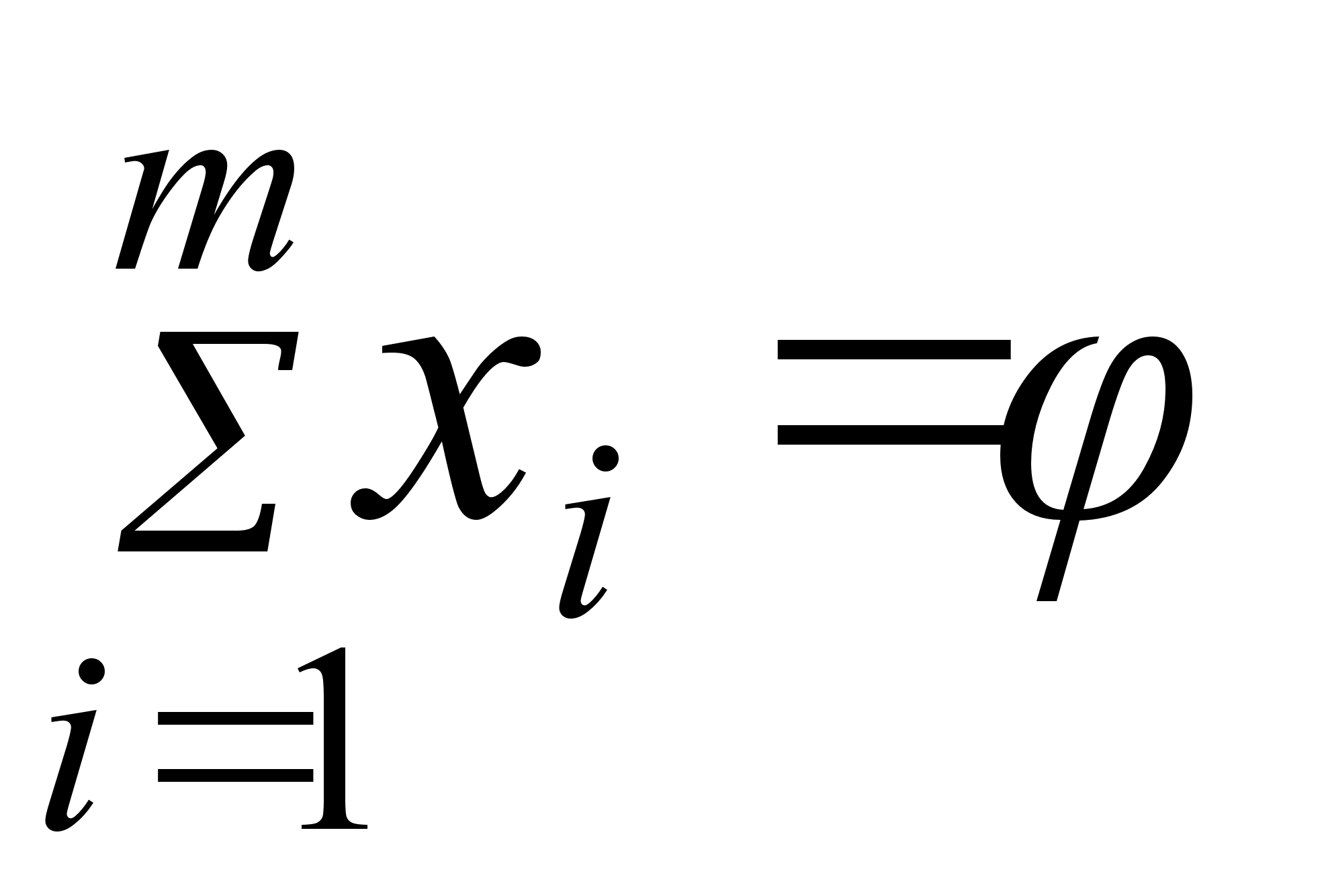
i
=Хi*V
–c какой вероятностью
необходимо
нанять i-ую бригаду.
Целевая функция:
Х1+Х2+Х3+Х4+Х5+Х6MIN
Ограничения:
10,8*Х2+21,6*Х3+32,4*Х4+75,6*Х5+86,4*Х61
46*Х1+36*Х2+46,8*Х3+57,6*Х4+100,8*Х5+111,6*Х61
100*Х1+86*Х2+72*Х3+82,8*Х4+126*Х5+136,8*Х61
162*Х1+144*Х2+126*Х3+108*Х4+151,2*Х5+162*Х61
392*Х1+372*Х2+352*Х3+332*Х4+252*Х5+262,8*Х61
480*Х1+456*Х2+432*Х3+408*Х4+312*Х5+288*Х61
Хi0;
Решив данную задачу линейного программирования на ПВЭМ, получим минимальное значение целевой функции φ=0,011574 и значения Xi:
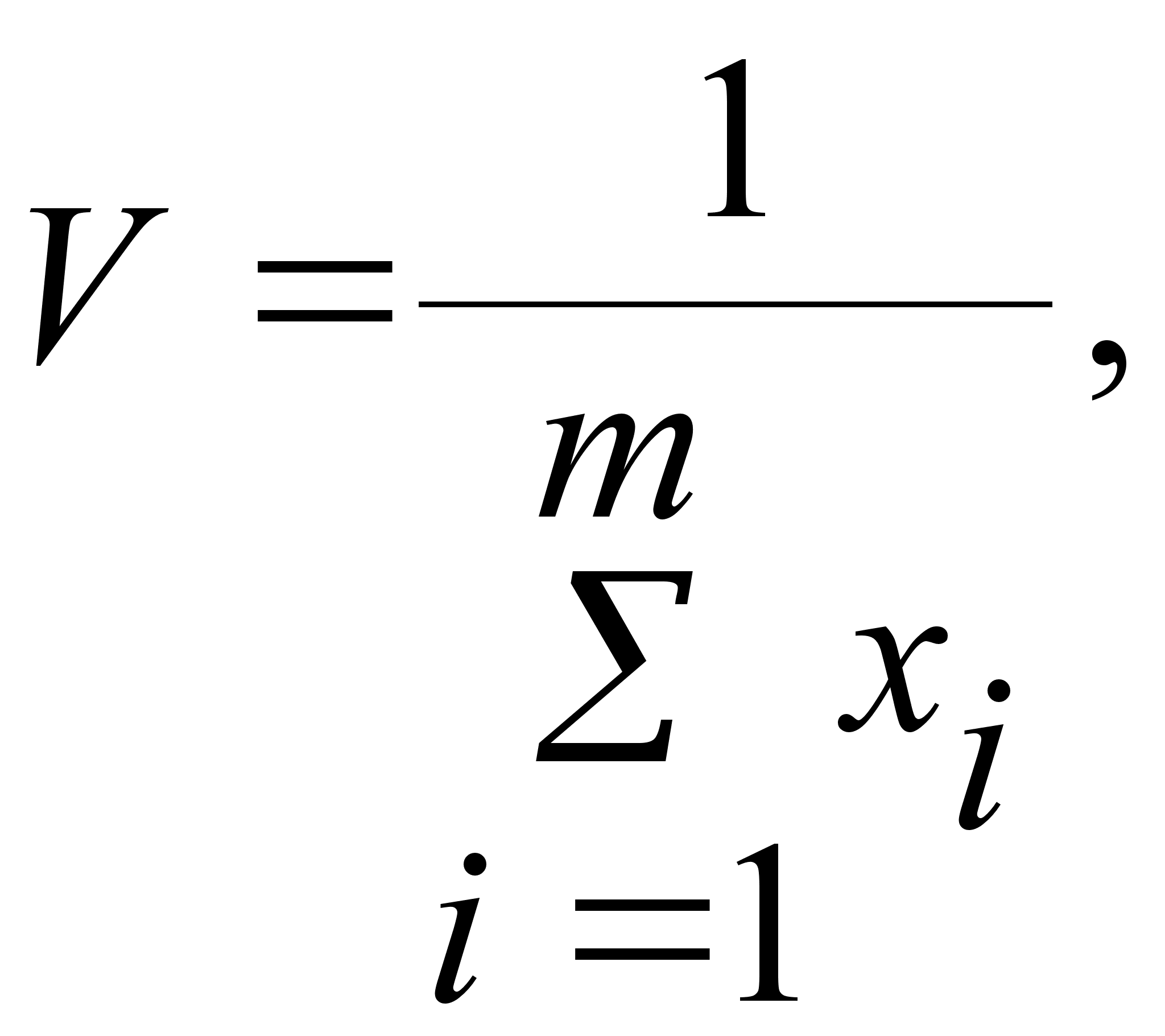Х1=0,
Х2=0,
Х3=0,
Х4=0,
Х5=0,
Х6=0,01157407.
Затем, используя формулу
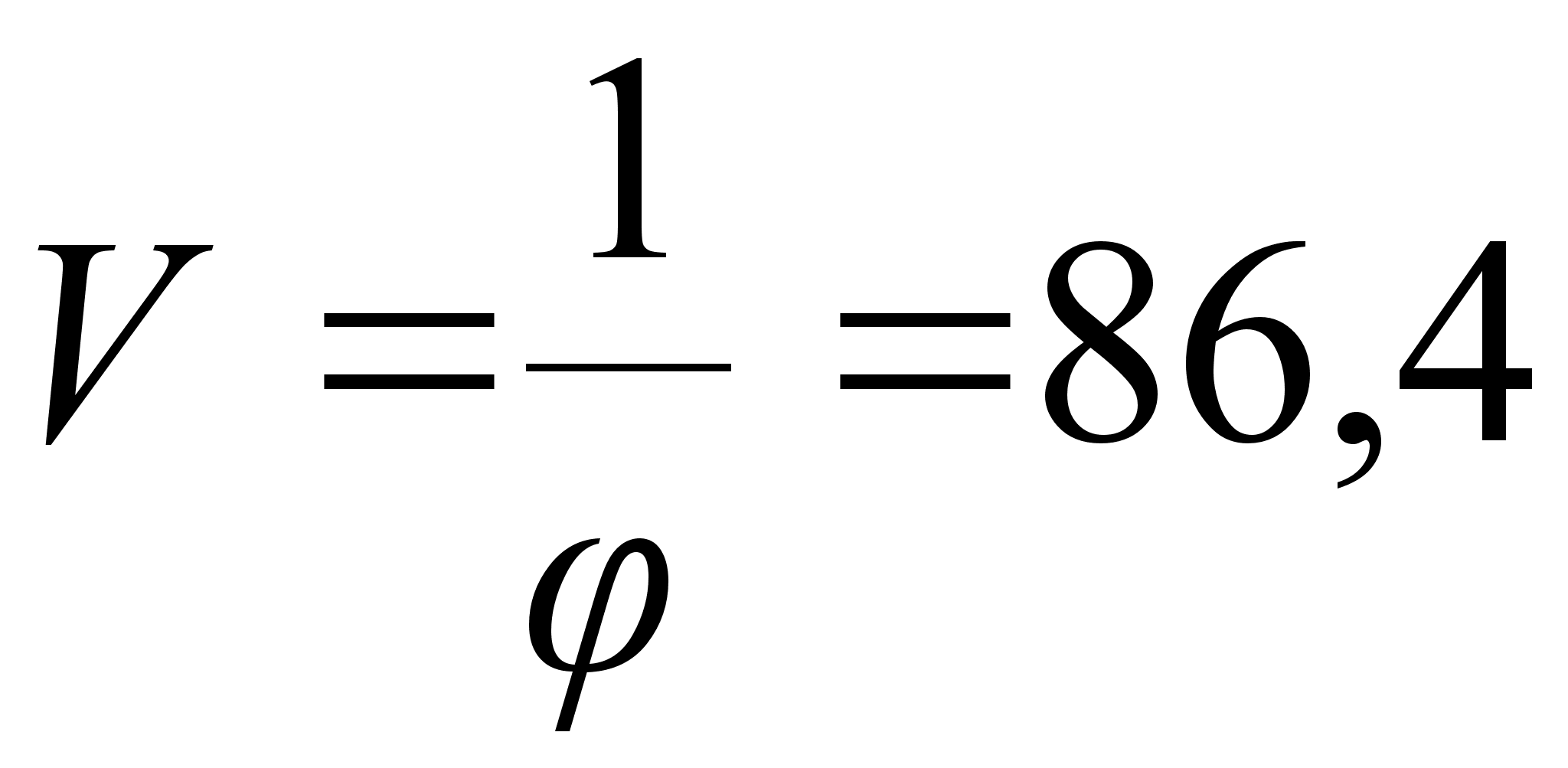
определим цену игры
Р6=0,01157407*86,4=1.
Это значит, что наименьший убыток Директор получит при применении
стратегии A6 при любом уровне производства.
Двойственная задача:
qj =Yj*V– вероятность i-го уровня производства (i=1,2,…,6).
Целевая функция:
Y1+Y2+Y3+Y4+Y5+Y6MAX
Ограничения:
46*Y2+100*Y3+162*Y4+392*Y5+480*Y6≤1
10,8*Y1+36*Y2+86*Y3+144*Y4+372*Y5+456*Y6≤1
21,6*Y1+46,8*Y2+72*Y3+126*Y4+352*Y5+432*Y6≤1
32,4*Y1+57,6*Y2+82,8*Y3+108*Y4+332*Y5+408*Y6≤1
75,6*Y1+100,8*Y2+126*Y3+151,2*Y4+252*Y5+312*Y6≤1
86,4*Y1+111,6*Y2+136,8*Y3+162*Y4+262,8*Y5+288*Y6≤1
Yj0;
7. Программа (листинг)
Программа находит оптимальную стратегию по критерию Вальда.
program Natasha;
uses crt;
var
d,m,n,i,j,L:integer;
MAX:REAL;
a:array[1..6,1..6] of real;
b,c,min:array[1..6] of real;
begin
l:=1;
clrscr;
write('Введите n: ');
readln(N);
WRITELN(' Введите цену одного рабочего при i-ом уровне производства');
FOR I:=1 TO n DO
BEGIN
WRITE('B',I,'=');
READLN(b[I]);
END;
writeln('Введите число нанимаемых рабочих при j-ом уровне производства');
FOR j:=1 TO n DO
BEGIN
WRITE('A',j,'=');
READLN(c[j]);
END;
write('Зарплата вне сезона: ');
readln(d);
FOR I:=1 TO n DO
BEGIN
FOR j:=1 TO n DO
BEGIN
if c[i]
else a[i,j]:=-(d*c[i]-(c[i]-c[j])*d*0.7);
END
END;
for i:=1 to n do
begin
for j:=1 to n do
write(' ',a[i,j]:5:1);
writeln(' ');
end;
for i:=1 to n do begin
min[i]:=a[i,1];
for j:=1 to n do if min[i]>a[i,j] then min[i]:=a[i,j];
if i=1 then max:=min[1];
if max
end;
WRITELN('По кpитерию Вальда оптимальная ',L,'-я стpатегия,MAX сpедний pиск=',MAX:8:3);
end.
8. Решение задачи, выданное программой.
В результате выполнения программы по условию этой задачи получили такой ответ: "По кpитерию Вальда оптимальная 6-я стpатегия, MAX сpедний выигрыш = -1008".
9. Вывод:
в результате анализа предложенной ситуации мы пришли к выводу, что Директору консервного завода имеет смысл применять 4-ю стратегию по критерию Байеса, 5-ю - по критериям Сэвиджа и Лапласа и 6-ю - по критерию Гурвица и Вальда. Директору завода можно порекомендовать придерживаться стратегии A4(по критерию Байеса), т.е. нанимать не менее 23-х рабочих вне сезона, т.к. в данном критерии высчитывается средний выигрыш игрока A с учетом вероятностей состояния природы.
Overview
Лист1Лист2
Sheet 1: Лист1
| Данные | Погода | мин выйгр фермера | ||||||||
| Вариант | 21 | 1 | 2 | 3 | 4 | 5 | ||||
| с01= | 60 | Культуры | 1 | 1267.5 | 2130.38 | 2476.5 | 2305.88 | 1618.5 | 1267.5 | |
| с02= | 30 | 2 | 1759.5 | 2932.5 | 3391.5 | 3136.5 | 2167.5 | 1759.5 | ||
| с03= | 75 | 3 | 1971 | 3260.25 | 3753 | 3449.25 | 2349 | 1971 | ||
| с04= | 25 | 4 | 1771 | 2909.5 | 3335 | 3047.5 | 2047 | 1771 | ||
| с05= | 60 | 5 | 1579.5 | 2578.88 | 2944.5 | 2676.38 | 1774.5 | 1579.5 | ||
| с06= | 40 | 6 | 2592.5 | 4209 | 4788.5 | 4331 | 2836.5 | 2592.5 | ||
| q1= | 0.43 | макс проигр природы | 2592.5 | 4209 | 4788.5 | 4331 | 2836.5 | 2592.5 | ||
| q2= | -0.06 | стратегия | A6 | оптимальна | ||||||
| q3= | 0.5 | |||||||||
| q4= | -0.15 | 1325 | 2078.63 | 2312 | 2025.13 | 1218 | 2312 | |||
| q5= | 0.28 | 833 | 1276.5 | 1397 | 1194.5 | 669 | 1397 | |||
| a= | 0.7 | 621.5 | 948.75 | 1035.5 | 881.75 | 487.5 | 1035.5 | |||
| 821.5 | 1299.5 | 1453.5 | 1283.5 | 789.5 | 1453.5 | |||||
| 1013 | 1630.13 | 1844 | 1654.63 | 1062 | 1844 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | |||||
| По критерию Сэвиджа оптимальна стратегия | A6 | 0 | ||||||||
| A1= | 1267.5 | 1760.3 | ||||||||
| A2= | 1759.5 | 2409.54 | ||||||||
| A3= | 1971 | 2665.21 | ||||||||
| A4= | 1771 | 2367.42 | ||||||||
| A5= | 1579.5 | 2089.45 | ||||||||
| A6= | 2592.5 | Стратегия А6 оптимальна | 3396.81 | Стратегия А6 оптимальна | ||||||
| критерий Вальда | 2592.5 | критерий Байеса | 3396.81 | |||||||
| A1= | 1959.75 | |||||||||
| A2= | 2677.5 | |||||||||
| A3= | 2956.5 | |||||||||
| A4= | 2622 | |||||||||
| A5= | 2310.75 | |||||||||
| A6= | 3751.5 | Стратегия А6 оптимальна | ||||||||
| критерий Лапласа | 3751.5 | |||||||||
| A1= | 1630.2 | |||||||||
| A2= | 2249.1 | |||||||||
| A3= | 2505.6 | |||||||||
| A4= | 2240.2 | |||||||||
| A5= | 1989 | |||||||||
| A6= | 3251.3 | Стратегия А6 оптимальна | ||||||||
| критерий Гурвица | 3251.3 | |||||||||
Sheet 2: Лист2
| 1267.5 | 2130.38 | 2476.5 | 2305.88 | 1618.5 | |||||
| 1759.5 | 2932.5 | 3391.5 | 3136.5 | 2167.5 | |||||
| 1971 | 3260.25 | 3753 | 3449.25 | 2349 | |||||
| 1771 | 2909.5 | 3335 | 3047.5 | 2047 | |||||
| 1579.5 | 2578.88 | 2944.5 | 2676.38 | 1774.5 | |||||
| 2592.5 | 4209 | 4788.5 | 4331 | 2836.5 | |||||
| max aij= | 4788.5 | ||||||||
| Задача ЛП | Двойственная задача | ||||||||
| Oграничения | Y1 | Y2 | Y3 | Y4 | Y5 | ||||
| 1 | 1.62 | 1.85 | 1.67 | 1.09 | 0 | 0 | 0 | 0 | 0 |
| X1= | 0 | Целевая функция | Ограничения | 0.49 | Целевая функция | ||||
| X2= | 0 | f= | 0 | 0.68 | f= | 0 | |||
| X3= | 0 | 0.76 | |||||||
| X4= | 0 | V= | 2592.5 | 0.68 | V= | 2592.5 | |||
| X5= | 0 | 0.61 | |||||||
| X6= | 0 | 1 | |||||||
