Реферат: «Нечеткая логика в системах управления»

Реферат: «Нечеткая логика в системах управления»

Московская Государственная Академия Приборостроения и Информатики

РЕФЕРАТ

по теория систем и системного анализа

«Нечеткая логика в системах управления»

Выполнил: Пяров Тимур Р
ЭФ2, 2 курс, 35.14

2002
Москва
Оглавление

Нечеткая логика в системах управления. 3

Немного теории. 3

Фаззификация (переход к нечеткости) 5

Лингвистические переменные. 6

Функции принадлежности. 6

Разработка нечетких правил. 7

Дефаззификация (устранение нечеткости) 8

Метод центра максимума (СоМ) 9

Метод наибольшего значения (МоМ) 9

Метод центроида (СоА) 9

Описание системы.. 10

Off-line-оптимизация. 11

On-line-оптимизация. 11

Реализация. 11

Литература. 13

Нечеткая логика в системах управления

В последнее время нечеткая технология завоевывает все больше сторонников среди разработчиков систем управления. Взяв старт в 1965 году из работ профессора Лотфи Заде [1], за прошедшее время нечеткая логика прошла путь от почти антинаучной теории, практически отвергнутой в Европе и США, до банальной ситуации конца девяностых годов, когда в Японии в широком ассортименте появились «нечеткие» бритвы, пылесосы, фотокамеры [4, 10]. Сам термин «fuzzy» так прочно вошел в жизнь, что на многих языках он даже не переводится. В России в качестве примера можно вспомнить рекламу стиральных машин и микроволновых печей фирмы Samsung, обладающих искусственным интеллектом на основе нечеткой логики.
Тем не менее, столь масштабный скачок в развитии нечетких систем управления не случаен. Простота и дешевизна их разработки заставляет проектировщиков все чаще прибегать к этой технологии. Бурный рост рынка нечетких систем 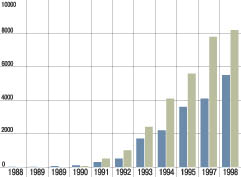показан на рис. 1.
После поистине взрывного старта прикладных нечетких систем в Японии [2, 3, 5, 6] многие разработчики США и Европы наконец-то обратили внимание на эту технологию. Но время было упущено, и мировым лидером в области нечетких систем стала Страна восходящего солнца [7, 8], где к концу 1980-х годов был налажен выпуск специализированных нечетких контроллеров, выполненных по технологии СБИС [9]. В такой ситуации Intel нашла поистине гениальное решение. Имея большое количество разнообразных контроллеров от MCS-51 до MCS-96, которые на протяжении многих лет успешно использовались во многих приложениях, корпорация решила создать средство разработки приложений на базе этих контроллеров, но с использованием технологии нечеткости. Это позволило избежать значительных затрат на конструирование собственных нечетких контроллеров, а система от Intel, получившая название fuzzy TECH, завоевала огромную популярность не только в США и Европе, но и прорвалась на японский рынок.

Немного теории

Нечеткая логика основана на использовании таких оборотов естественного языка, как «далеко», «близко», «холодно», «горячо». Диапазон ее применения очень широк - от бытовых приборов до управления сложными промышленными процессами. Многие современные задачи управления просто не могут быть решены классическими методами из-за очень большой сложности математических моделей, их описывающих. Вместе с тем, чтобы использовать теорию нечеткости на цифровых компьютерах, необходимы математические преобразования, позволяющие перейти от лингвистических переменных к их числовым аналогам в ЭВМ.

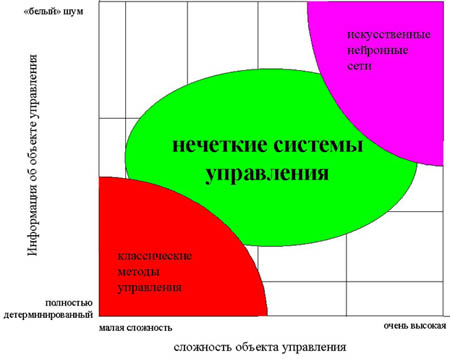
На рис. 2 показаны области наиболее эффективного применения современных технологий управления. Как видно, классические методы управления хорошо работают при полностью детерминированном объекте управления и детерминированной среде, а для систем с неполной информацией и высокой сложностью объекта управления оптимальными являются нечеткие методы управления. (В правом верхнем углу рисунка приведена еще одна современная технология управления - с применением искусственных нейронных сетей, но мы не станем столь глубоко вдаваться в достижения ученых.)

Вернемся к теории и кратко рассмотрим такие понятия, как «нечеткие правила», «нечеткий вывод» да и сам термин «нечеткое управление».

Классическая логика развивается с древнейших времен. Ее основоположником считается Аристотель. Логика известна нам как строгая и сугубо теоретическая наука, и большинство ученых (кроме разработчиков последнего поколения компьютеров) продолжают придерживаться этого мнения. Вместе с тем классическая или булева логика имеет один существенный недостаток - с ее помощью невозможно описать ассоциативное мышление человека. Классическая логика оперирует только двумя понятиями: ИСТИНА и ЛОЖЬ, и исключая любые промежуточные значения. Аналогично этому булева логика не признает ничего кроме единиц и нулей. Все это хорошо для вычислительных машин, но попробуйте представить весь окружающий вас мир только в черном и белом цвете, вдобавок исключив из языка любые ответы на вопросы, кроме ДА и НЕТ. В такой ситуации вам можно только посочувствовать. Решить эту проблему и призвана нечеткая логика. С термином «лингвистическая переменная» можно связать любую физическую величину, для которой нужно иметь больше значений, чем только ДА и НЕТ. В этом случае вы определяете необходимое число термов и каждому из них ставите в соответствие некоторое значение описываемой физической величины. Для этого значения степень принадлежности физической величины к терму будет равна единице, а для всех остальных значений - в зависимости от выбранной функции принадлежности. Например, можно ввести переменную ВОЗРАСТ и определить для нее термы ЮНОШЕСКИЙ, СРЕДНИЙ и ПРЕКЛОННЫЙ. Обсудив с экспертами значения конкретного возраста для каждого терма, вы с полной уверенностью можете избавиться от жестких ограничений логики Аристотеля.

Получившие наибольшее развитие из всех разработок искусственного интеллекта, экспертные системы завоевали устойчивое признание в качестве систем поддержки принятия решений. Подобные системы способны аккумулировать знания, полученные человеком в различных областях деятельности. Посредством экспертных систем удается решить многие современные задачи, в том числе и задачи управления. Однако большинство систем все еще сильно зависит от классической логики.

Одним из основных методов представления знаний в экспертных системах являются продукционные правила, позволяющие приблизиться к стилю мышления человека. Любое правило продукций состоит из посылок и заключения. Возможно наличие нескольких посылок в правиле, в этом случае они объединяются посредством логических связок И, ИЛИ. Обычно продукционное правило записывается в виде: «ЕСЛИ (посылка) (связка) (посылка)… (посылка) ТО (заключение)».

Главным же недостатком продукционных систем остается то, что для их функционирования требуется наличие полной информации о системе.

Нечеткие системы тоже основаны на правилах продукционного типа, однако в качестве посылки и заключения в правиле используются лингвистические переменные, что позволяет избежать ограничений, присущих классическим продукционным правилам.

Целевая установка процесса управления связывается с выходной переменной нечеткой системы управления, но результат нечеткого логического вывода является нечетким, а физическое исполнительное устройство не способно воспринять такую команду. Необходимы специальные математические методы, позволяющие переходить от нечетких значений величин к вполне определенным. В целом весь процесс нечеткого управления можно разбить на несколько шагов: фаззификация, разработка нечетких правил и дефаззификация.

Рассмотрим подробнее эти шаги на примере поставляемой с пакетом fuzzy TECH модели контейнерного крана. Пусть вам, как маститому крановщику, необходимо перегрузить контейнер с баржи на железнодорожную платформу. Вы управляете мощностью двигателя тележки крана, заставляя ее двигаться быстрее или медленнее. От скорости перемещения тележки, в свою очередь, зависит расстояние до цели и амплитуда колебания контейнера на тросе. Вследствие того, что стратегия управления краном сильно зависит от положения тележки, применение стандартных контроллеров для этой задачи весьма затруднительно. Вместе с тем математическая модель движения груза, состоящая из нескольких дифференциальных уравнений, может быть составлена довольно легко, но для ее решения при различных исходных данных потребуется довольно много времени. К тому же исполняемый код программы будет большим и не поворотливым. Нечеткая система справляется с такой задачей очень быстро - несмотря на то, что вместо сложных дифференциальных уравнений движения груза весь процесс движения описывается терминами естественного языка: «больше», «средне», «немного» и т. п. То есть так, будто вы даете указания своему товарищу, сидящему за рычагами управления.

Фаззификация (переход к нечеткости)

Точные значения входных переменных преобразуются в значения лингвистических переменных посредством применения некоторых положений теории нечетких множеств, а именно - при помощи определенных функций принадлежности.

Рассмотрим этот этап подробнее. Прежде всего, введем понятие «лингвистической переменной» и «функции принадлежности».

Лингвистические переменные

В нечеткой логике значения любой величины представляются не числами, а словами естественного языка и называются ТЕРМАМИ. Так, значением лингвистической переменной ДИСТАНЦИЯ являются термы ДАЛЕКО, БЛИЗКО и т. д.

Страницы: 1, 2